《2025年课时练作业与测评九年级数学上册冀教版》

8. 等腰三角形一条边的长为3，它的另两条边的长是关于x的一元二次方程x²-12x+k=0的两个根，则k的值是( )

A.27
B.36
C.27或36
D.18

答案： 8.B

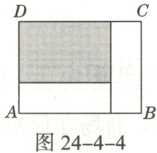
9. 如图24-4-4，矩形ABCD是由三个矩形拼接成的.如果AB=8，阴影部分的面积是24，另外两个小矩形全等，那么小矩形的长为_________.

答案： 9.6

10. 已知长方形硬纸板ABCD的长BC为40cm，宽CD为30cm，按图24-4-5所示剪掉2个小正方形和2个小长方形(即图中阴影部分)，将剩余部分折成一个有盖的长方体盒子，设剪掉的小正方形的边长为x cm.(纸板的厚度忽略不计)
(1)填空：EF=______cm，GH=______cm. (用含x的代数式表示)
(2)若折成的长方体盒子的表面积为950cm²，求该长方体盒子的体积.
]

答案： 10.解：
(1)$EF=(30 - 2x)cm,GH=(20 - x)cm$。
故答案为$(30 - 2x),(20 - x)$。
(2)根据题意，得$40×30 - 2x^{2}-2×20x = 950$，
解得$x_{1}=5,x_{2}=-25$（不合题意，舍去），
所以长方体盒子的体积$=x(30 - 2x)(20 - x)=5×20×15 = 1500(cm^{3})$。
答：长方体盒子的体积为$1500cm^{3}$。

11. 如图24-4-6，在Rt△ABC中，∠C=90°，AC=6cm，BC=8cm，点P从C点出发，以每秒1cm的速度向A点移动，同时，点Q从C点出发，以每秒2cm的速度向B点移动，那么______s后，△PCQ的面积为5cm².

答案： 11.$\sqrt{5}$

12. 用长为32m的篱笆围一个矩形养鸡场，设围成的矩形一边长为x m，面积为y m².
(1)求y关于x的函数关系式.
(2)当x为何值时，围成的养鸡场的面积为60m²？
(3)能否围成面积为70m²的养鸡场？如果能，请求出其边长；如果不能，请说明理由.

答案： 12.解：
(1)$y = x(16 - x)=-x^{2}+16x(0\lt x\lt16)$。
(2)当$y = 60$时，$-x^{2}+16x = 60$，解得$x_{1}=10,x_{2}=6$，
所以当$x$为10或6时，围成的养鸡场的面积为$60m^{2}$。
(3)不能。
理由如下：
当$y = 70$时，$-x^{2}+16x = 70$，
整理，得$x^{2}-16x + 70 = 0$。
因为$\Delta=256 - 280=-24\lt0$，
所以此方程无解，所以不能围成面积为$70m^{2}$的养鸡场。