《2025年高中同步测控优化训练高中数学必修第二册人教B》

7. 已知 $ P(A) = 0.3 $，$ P(B) = 0.5 $，当事件 $ A $，$ B $ 相互独立时，$ P(A + B) = $0.65，$ P(A\overline{B}) = $0.15。

答案： 7.0.65 0.15 解析：
∵A，B相互独立，
∴P(A+B)=P(A)+P(B)-P(A)·P(B)=0.3+0.5-0.3×0.5=0.65.
$P(A\overline{B})=P(A)P(\overline{B})=0.3×(1-0.5)=0.15.$

8. 设两个相互独立的事件 $ A $，$ B $ 都不发生的概率为 $ \frac{1}{9} $，$ A $ 发生 $ B $ 不发生的概率等于 $ B $ 发生 $ A $ 不发生的概率，则事件 $ A $ 发生的概率 $ P(A) = $\frac{2}{3}。

答案： $8.\frac{2}{3} $解析：由已知可得$\begin{cases} [1-P(A)][1-P(B)]=\frac{1}{9}, \\ P(A)[1-P(B)]=P(B)[1-P(A)], \end{cases}$
解得$P(A)-P(B)=\frac{2}{3}.$

9. 在同一时间内，两个气象台预报天气准确的概率分别为 $ \frac{9}{10} $，$ \frac{4}{5} $，两个气象台预报准确的概率互不影响，则在同一时间内，至少有一个气象台预报准确的概率为\frac{49}{50}。

答案： $9.\frac{49}{50} $解析：$P=1-(1-\frac{9}{10})(1-\frac{4}{5})=\frac{49}{50}$

10. 某班准备到郊外野营，为此向商店定了帐篷，如果下雨与不下雨是等可能的，能否准时收到帐篷是等可能的，只要帐篷如期运到，他们就不会淋雨，则淋雨的概率是$\frac{1}{4}$。

答案： $10.\frac{1}{4} $解析：下雨概率为$\frac{1}{2}，$不下雨概率为$\frac{1}{2}，$收到帐篷概率为$\frac{1}{2}，$收不到帐篷概率为$\frac{1}{2}，$当下雨且收不到帐篷时会淋雨，所以淋雨的概率为$\frac{1}{2}×\frac{1}{2}=\frac{1}{4}.$

11. 已知 $ A $，$ B $，$ C $ 为三个独立事件，若事件 $ A $ 发生的概率是 $ \frac{1}{2} $，事件 $ B $ 发生的概率是 $ \frac{2}{3} $，事件 $ C $ 发生的概率是 $ \frac{3}{4} $，求下列事件的概率：
（1）事件 $ A $，$ B $，$ C $ 只发生两个；
（2）事件 $ A $，$ B $，$ C $ 至多发生两个。

答案： 11.解：
(1)记“事件A，B，C只发生两个”为$A_1，$则事件$A_1$包括三种彼此互斥的情况，$ABC;\overline{A}BC;A\overline{B}C;AB\overline{C}.$由互斥事件概率的加法公式和相互独立事件的概率乘法公式，得$P(A_1)=P(A\overline{B}C)+P(\overline{A}BC)+P(AB\overline{C})=\frac{1}{12}+\frac{1}{8}+\frac{1}{4}=\frac{11}{24},$故事件A，B，C只发生两个的概率为$\frac{11}{24}$
(2)记“事件A，B，C至多发生两个”为$A_2，$则包括彼此互斥的三种情况：事件A，B，C一个也不发生，记为$A_3，$事件A，B，C只发生一个，记为$A_4，$事件A，B，C只发生两个，记为$A_5，$故$P(A_2)=P(A_3)+P(A_4)+P(A_5)=\frac{1}{24}+\frac{6}{24}+\frac{11}{24}=\frac{3}{4}$
∴事件A，B，C至多发生两个的概率为$\frac{3}{4}$

12. 某公司为了解用户对其产品的满意度，从 $ A $，$ B $ 两地区分别随机调查了 20 个用户，得到用户对产品的满意度评分如下：
$ A $ 地区：62 73 81 92 95 85 74 64 53 76 78 86 95 66 97 78 88 82 76 89
$ B $ 地区：73 83 62 51 91 46 53 73 64 82 93 48 65 81 74 56 54 76 65 79
（1）根据两组数据完成两地区用户满意度评分的茎叶图，并通过茎叶图比较两地区满意度评分的平均值及分散程度（不要求计算出具体值，给出结论即可）；

（2）根据用户满意度评分，将用户的满意度从低到高分为三个等级：

记事件 $ C $：“$ A $ 地区用户的满意度等级高于 $ B $ 地区用户的满意度等级”。假设两地区用户的评价结果相互独立。根据所给数据，以事件发生的频率作为相应事件发生的概率，求 $ C $ 的概率。

答案：
$(1)$ 绘制茎叶图并比较
- 绘制茎叶图：

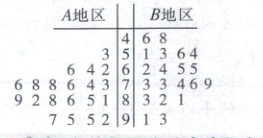
- 比较平均值及分散程度：
通过茎叶图可以看出，$A$地区用户满意度评分的平均值高于$B$地区用户满意度评分的平均值；$A$地区用户满意度评分比较集中，$B$地区用户满意度评分比较分散。
$(2)$ 计算$P(C)$
解：
设$A_1$表示“$A$地区用户的满意度等级为满意或非常满意”，$A_2$表示“$A$地区用户的满意度等级为非常满意”，$B_1$表示“$B$地区用户的满意度等级为不满意”，$B_2$表示“$B$地区用户的满意度等级为满意”。
则$C = A_1B_1 + A_2B_2$，且$A_1$与$B_1$，$A_2$与$B_2$相互独立。
由所给数据得，$A$地区用户满意度等级为满意或非常满意的频率为$\frac{16}{20}=\frac{4}{5}$，$A$地区用户满意度等级为非常满意的频率为$\frac{4}{20}=\frac{1}{5}$，$B$地区用户满意度等级为不满意的频率为$\frac{10}{20}=\frac{1}{2}$，$B$地区用户满意度等级为满意的频率为$\frac{8}{20}=\frac{2}{5}$。
所以$P(A_1)=\frac{4}{5}$，$P(A_2)=\frac{1}{5}$，$P(B_1)=\frac{1}{2}$，$P(B_2)=\frac{2}{5}$。
故$P(C)=P(A_1B_1 + A_2B_2)=P(A_1)P(B_1)+P(A_2)P(B_2)=\frac{4}{5}×\frac{1}{2}+\frac{1}{5}×\frac{2}{5}=\frac{4}{10}+\frac{2}{25}=\frac{20 + 4}{50}=\frac{24}{50}=\frac{12}{25}$。
综上，$(1)$ $A$地区用户满意度评分的平均值高于$B$地区用户满意度评分的平均值；$A$地区用户满意度评分比较集中，$B$地区用户满意度评分比较分散。$(2)$ $\boldsymbol{\frac{12}{25}}$ 。