2025年高中同步测控优化训练高中数学必修第二册人教B
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年高中同步测控优化训练高中数学必修第二册人教B 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
7. (多选)已知集合$A$是集合$B$的真子集,下列关于非空集合$A$,$B$的四个命题:
①若任取$x\in A$,则$x\in B$是必然事件:
②若任取$x\notin A$,则$x\in B$是不可能事件;
③若任取$x\in B$,则$x\in A$是随机事件;
④若任取$x\notin B$,则$x\notin A$是必然事件。
其中正确的命题有(
A.①
B.②
C.③
D.④
①若任取$x\in A$,则$x\in B$是必然事件:
②若任取$x\notin A$,则$x\in B$是不可能事件;
③若任取$x\in B$,则$x\in A$是随机事件;
④若任取$x\notin B$,则$x\notin A$是必然事件。
其中正确的命题有(
ACD
)A.①
B.②
C.③
D.④
答案:
7.ACD 解析:因为集合A是集合B的真子集,所以集合A中的元素都在集合B中,集合B中存在元素不是集合A中的元素,作出其韦恩图如图:
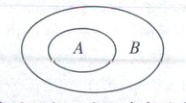
对于③:因为集合A是集合B的真子集,集合B中存在元素不是集合A中的元素,集合B中也存在集合A中的元素,所以任取x∈B,则x∈A是随机事件,故③正确;
对于④:因为集合A中的任何一个元素都是集合B中的元素,任取x∉B,则x∉A是必然事件,故④正确;所以①③④正确.
故选ACD.
7.ACD 解析:因为集合A是集合B的真子集,所以集合A中的元素都在集合B中,集合B中存在元素不是集合A中的元素,作出其韦恩图如图:

对于③:因为集合A是集合B的真子集,集合B中存在元素不是集合A中的元素,集合B中也存在集合A中的元素,所以任取x∈B,则x∈A是随机事件,故③正确;
对于④:因为集合A中的任何一个元素都是集合B中的元素,任取x∉B,则x∉A是必然事件,故④正确;所以①③④正确.
故选ACD.
8. 从存放号码分别为 1,2,3,…,10 的卡片的盒里,有放回地取 100 次,每次取一张卡片,并记下号码,统计结果如下:
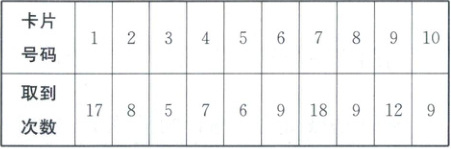
取到号码为奇数的样本点有

取到号码为奇数的样本点有
58
个。
答案:
8.58 解析:根据表格结合样本点的概念可知取到奇数号码的次数为58,故取到号码为奇数的样本点为58.
9. 在掷骰子的试验中,可以得到以下事件:
$A = \{出现 1 点\}$;$B = \{出现 2 点\}$;$C = \{出现 3 点\}$;$D = \{出现 4 点\}$;$E = \{出现 5 点\}$;$F = \{出现 6 点\}$;$G = \{出现的点数不大于 1\}$;$H = \{出现的点数小于 5\}$;$I = \{出现奇数点\}$;$J = \{出现偶数点\}$。请根据这些事件,判断下列事件的关系:
(1)$B$
(3)$E$
$A = \{出现 1 点\}$;$B = \{出现 2 点\}$;$C = \{出现 3 点\}$;$D = \{出现 4 点\}$;$E = \{出现 5 点\}$;$F = \{出现 6 点\}$;$G = \{出现的点数不大于 1\}$;$H = \{出现的点数小于 5\}$;$I = \{出现奇数点\}$;$J = \{出现偶数点\}$。请根据这些事件,判断下列事件的关系:
(1)$B$
⊆
$H$;(2)$D$⊆
$J$;(3)$E$
⊆
$I$;(4)$A$=
$G$。
答案:
9.
(1)⊆
(2)⊆
(3)⊆
(4)= 解析:当事件B发生时,事件H必然发生,故B⊆H;同理D⊆J,E⊆I.易知事件A与事件G相等,即A=G.
(1)⊆
(2)⊆
(3)⊆
(4)= 解析:当事件B发生时,事件H必然发生,故B⊆H;同理D⊆J,E⊆I.易知事件A与事件G相等,即A=G.
10. 给出以下三个命题:(1)将一枚质地均匀地硬币抛掷两次,记事件$A$:“二次都出现正面”,事件$B$:“二次都出现反面”,则事件$A$与事件$B$是对立事件;(2)在命题(1)中,事件$A$与事件$B$是互斥事件;(3)在 10 件产品中有 3 件是次品,从中任取 3 件,记事件$A$:“所取 3 件中最多有 2 件是次品”,事件$B$:“所取 3 件中至少有 2 件是次品”,则事件$A$与事件$B$是互斥事件,其中真命题的个数是
三、解答题
1
个。三、解答题
答案:
10.1 解析:命题
(1)是假命题,命题
(2)是真命题,命题
(3)是假命题,对于
(1)
(2),因为抛掷两次硬币,除事件A,B外,还有“第一次出现正面,第二次出现反面”和“第一次出现反面,第二次出现正面”两个事件,所以事件A和事件B不是对立事件,但它们不会同时发生,所以是互斥事件;对于
(3),若所取的3件产品中恰有2件次品,则事件A和事件B同时发生,所以事件A和事件B不是互斥事件.
(1)是假命题,命题
(2)是真命题,命题
(3)是假命题,对于
(1)
(2),因为抛掷两次硬币,除事件A,B外,还有“第一次出现正面,第二次出现反面”和“第一次出现反面,第二次出现正面”两个事件,所以事件A和事件B不是对立事件,但它们不会同时发生,所以是互斥事件;对于
(3),若所取的3件产品中恰有2件次品,则事件A和事件B同时发生,所以事件A和事件B不是互斥事件.
11. 从含有两件正品$a_{1}$,$a_{2}$和一件次品$b_{1}$的三件产品中,每次任取一件,每次取出后不放回,前后取两次。
(1)写出这个试验的样本空间;
(2)$E_{2}$:取出两件产品中恰有一件次品,写出$E_{2}$的样本空间。
(1)写出这个试验的样本空间;
(2)$E_{2}$:取出两件产品中恰有一件次品,写出$E_{2}$的样本空间。
答案:
11.解:
(1)试验样本空间为:Ω₁={(a₁,a₂),(a₁,b₁),(a₂,b₁),(a₂,a₁),(b₁,a₁),(b₁,a₂)}.
(2)E₂的样本空间为:Ω₂={(a₁,b₁),(a₂,b₁),(b₁,a₁),(b₁,a₂)}.
(1)试验样本空间为:Ω₁={(a₁,a₂),(a₁,b₁),(a₂,b₁),(a₂,a₁),(b₁,a₁),(b₁,a₂)}.
(2)E₂的样本空间为:Ω₂={(a₁,b₁),(a₂,b₁),(b₁,a₁),(b₁,a₂)}.
12. 台风在危害人类的同时,也在保护人类。台风给人类送来了淡水资源,大大缓解了全球水荒,另外还使世界各地冷热保持相对均衡。甲、乙、丙三颗卫星同时监测台风,在同一时刻,甲、乙、丙三颗卫星准确预报台风的概率分别为 0.8,0.7,0.9,各卫星间相互独立,求在同一时刻至少有两颗预报准确的概率。
答案:
12.解:设甲、乙、丙预报准确依次记为事件A,B,C,不准确分别记为$\overline{A},\overline{B},\overline{C},$
则P(A)=0.8,P(B)=0
则P(A)=0.8,P(B)=0
查看更多完整答案,请扫码查看


