《2025年高中同步测控优化训练高中数学必修第二册人教B》

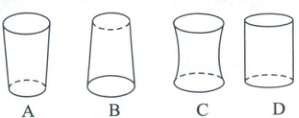
1. 向高为$H$的水瓶内注水，注满为止，如果注水量$V$与水深$h$的函数关系的图像如图所示，那么水瓶的形状是(B)

答案： 1.B

2. 若$x\in(1,2)$，则下列结论正确的是(A)

A.$2^{x}＞x^{\frac{1}{2}}＞\lg x$
B.$2^{x}＞\lg x＞x^{\frac{1}{2}}$
C.$x^{\frac{1}{2}}＞2^{x}＞\lg x$
D.$x^{\frac{1}{2}}＞\lg x＞2^{x}$

答案： 2.A

3. 某商场$2021$年一月份到十二月份销售额呈现先下降后上升的趋势，现有三种函数模型：
①$f(x)=p· q^{x}(q＞0,q\neq1)$；
②$f(x)=\log_{p}x + q(p＞0,p\neq1)$；
③$f(x)=x^{2}+px + q$.
能较准确反映商场月销售额$f(x)$与月份$x$关系的函数模型为③(填写相应函数的序号)，若所选函数满足$f(1)=10$，$f(3)=2$，则$f(x)=$x^2-8x+17.

答案： $3.③x^2-8x+17$

4. 函数$f(x)$的定义域为$A$，若$x_{1},x_{2}\in A$且$f(x_{1}) = f(x_{2})$时总有$x_{1}=x_{2}$，则称$f(x)$为单函数. 例如，函数$f(x)=x + 1(x\in\mathbf{R})$是单函数. 下列命题：①函数$f(x)=x^{2}-2x(x\in\mathbf{R})$是单函数；②函数$f(x)=\begin{cases}\log_{2}x,x\geq2,\\2 - x,x＜2\end{cases}$是单函数；③若$f(x)$为单函数，$x_{1},x_{2}\in A$且$x_{1}\neq x_{2}$，则$f(x_{1})\neq f(x_{2})$；④函数$f(x)$在定义域内某个区间$D$上具有单调性，则$f(x)$一定是单函数. 其中的真命题是 ______ (写出所有真命题的编号).

答案： 4.③ 解析：①若$f(x)=x^2-2x，$则由$f(x_1)=f(x_2)$得$x_1^2-2x_1=x_2^2-2x_2，$即$(x_1-x_2)(x_1+x_2-2)=0，$解得$x_1=x_2，$或$x_1+x_2-2=0，$所以①不是单函数.
②若$f(x)=\begin{cases}\log_2x,x\geq2,\\2-x,x\lt2,\end{cases}$
则由函数图像可知当$f(x_1)=f(x_2)$时，$x_1\neq x_2，$所以②不是单函数.
③根据单函数的定义可知，③正确.
④在定义域内某个区间D上具有单调性，单在整个定义域上不一定单调，所以④不一定正确.比如②函数，所以真命题为③.

5. 某公司为了实现$1000$万元的利润目标，准备制定一个激励销售人员的奖励方案：在销售利润达到$10$万元时，按销售利润进行奖励，且资金$y$（单位：万元）随销售利润$x$（单位：万元）的增加而增加，但资金总数不超过$5$万元，同时资金不超过利润的$25\%$. 现有三个奖励模型：$y = 0.25x$，$y=\log_{7}x + 1$，$y = 1.002^{x}$，其中哪个模型能符合公司的要求？

答案： 5.解：作出函数y=5，y=0.25x，$y=\log_7x+1，$y=1.002^x的图像(如图).
观察图像发现，在区间[10，1000]上，模型y=0.25x，y=1.002^x的图像都有一部分在直线y=5的上方，只有模型$y=\log_7x+1$的图像始终在y=5和y=0.25x的下方，这说明只有按模型$y=\log_7x+1$进行奖励时才符合公司的要求.

6. 我们知道：人们对声音有不同的感觉，这与它的强度有关系. 声音的强度用瓦/米$^{2}$表示，但在实际测量时，声音的强度水平常用$L_{1}$表示，它们满足以下公式：$L_{1}=10\lg\frac{I}{I_{0}}$（单位为分贝，$L_{1}\geq0$，其中$I_{0}=1×10^{-12}$瓦/米$^{2}$，是人们平均能听到的最小强度，是听觉的开端）. 回答下列问题：
(1)树叶沙沙声的强度是$1×10^{-12}$瓦/米$^{2}$，耳语的强度是$1×10^{-10}$瓦/米$^{2}$，恬静的无线电广播的强度是$1×10^{-8}$瓦/米$^{2}$，试分别求出它们的强度水平；
(2)某一新建的安静小区规定：小区内公共场所的声音的强度水平必须保持在$50$分贝以下，试求声音强度$I$的范围为多少？

答案： 6.解：
(1)由题意知：树叶沙沙声的强度水平$L_2=10\lg\frac{I_2}{I_0}=10\lg1=0($分贝)；
耳语的强度水平为$L_3=10\lg\frac{I_3}{I_0}=10\lg10^2=20($分贝)；
恬静的无线电广播的强度水平为$L_4=10\lg\frac{I_4}{I_0}=10\lg10^4=40($分贝).
(2)由题意知$0\leq L_1\lt50，$即$0\leq10\lg\frac{I}{I_0}\lt50，$
所以$1\leq\frac{I}{I_0}\lt10^5，$即$1×10^{-12}\leqI\lt1×10^{-7}.$
所以新建的安静小区的声音强度I的范围为$[1×10^{-12}，$$1×10^{-7}).$