2025年高中同步测控优化训练高中数学必修第二册人教B
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年高中同步测控优化训练高中数学必修第二册人教B 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
4. (多选)金枪鱼因为肉质柔嫩鲜美、营养丰富深受现代人喜爱,常被制作成罐头食用。但当这种鱼罐头中的汞含量超过 1.0 mg/kg 时,食用它就会对人体产生危害。某工厂现有甲、乙两条金枪鱼罐头生产线,现从甲、乙两条生产线中各随机选出 10 盒罐头并检验其汞含量(单位为 mg/kg),其中甲生产线数据统计如下:0.07,0.24,0.39,0.54,0.61,0.66,0.73,0.82,0.95,0.99,其方差为$s_{1}^{2}=0.08$。乙生产线统计数据的均值为$\overline{x}_{2}=0.4$,方差为$s_{2}^{2}=0.11$,下列说法正确的有(
A.甲生产线的金枪鱼罐头汞含量数值样本的上四分位数是 0.82
B.甲生产线的金枪鱼罐头汞含量数值样本的上四分位数是 0.775
C.由样本估计总体,甲生产线生产的金枪鱼罐头汞含量平均值高于两条生产线生产的金枪鱼罐头汞含量平均值
D.由样本估计总体,甲生产线生产的金枪鱼罐头汞含量数值较两条生产线生产的金枪鱼罐头汞含量数值更稳定
ACD
)A.甲生产线的金枪鱼罐头汞含量数值样本的上四分位数是 0.82
B.甲生产线的金枪鱼罐头汞含量数值样本的上四分位数是 0.775
C.由样本估计总体,甲生产线生产的金枪鱼罐头汞含量平均值高于两条生产线生产的金枪鱼罐头汞含量平均值
D.由样本估计总体,甲生产线生产的金枪鱼罐头汞含量数值较两条生产线生产的金枪鱼罐头汞含量数值更稳定
答案:
4.ACD 解析:AB选项,$10×0.75 = 7.5$,则从小到大排列,第$8$个数为上四分位 ,A正确,B错误;C选项,甲生产线数据平均数为$\frac{1}{10}×(0.07 + 0.24 + 0.39 + 0.54 + 0.61 + 0.73 + 0.82 + 0.95 + 0.99)=0.534$,故两条生产线生产的金枪鱼罐头汞含量为$\frac{0.534 + 0.4}{2}=0.467$,因为$0.534>0.467$,所以C正确。
,A正确,B错误;C选项,甲生产线数据平均数为$\frac{1}{10}×(0.07 + 0.24 + 0.39 + 0.54 + 0.61 + 0.73 + 0.82 + 0.95 + 0.99)=0.534$,故两条生产线生产的金枪鱼罐头汞含量为$\frac{0.534 + 0.4}{2}=0.467$,因为$0.534>0.467$,所以C正确。
D选项,甲、乙生产线生产的金枪鱼罐头汞含量方差分别为$s_{1}^{2}=0.08$,$s_{2}^{2}=0.11$,因为$0.08<0.11$,所以甲生产线生产的金枪鱼罐头汞含量数值较两条生产线生产的金枪鱼罐头汞含量数值更稳定,D正确。故选ACD。
4.ACD 解析:AB选项,$10×0.75 = 7.5$,则从小到大排列,第$8$个数为上四分位
 ,A正确,B错误;C选项,甲生产线数据平均数为$\frac{1}{10}×(0.07 + 0.24 + 0.39 + 0.54 + 0.61 + 0.73 + 0.82 + 0.95 + 0.99)=0.534$,故两条生产线生产的金枪鱼罐头汞含量为$\frac{0.534 + 0.4}{2}=0.467$,因为$0.534>0.467$,所以C正确。
,A正确,B错误;C选项,甲生产线数据平均数为$\frac{1}{10}×(0.07 + 0.24 + 0.39 + 0.54 + 0.61 + 0.73 + 0.82 + 0.95 + 0.99)=0.534$,故两条生产线生产的金枪鱼罐头汞含量为$\frac{0.534 + 0.4}{2}=0.467$,因为$0.534>0.467$,所以C正确。D选项,甲、乙生产线生产的金枪鱼罐头汞含量方差分别为$s_{1}^{2}=0.08$,$s_{2}^{2}=0.11$,因为$0.08<0.11$,所以甲生产线生产的金枪鱼罐头汞含量数值较两条生产线生产的金枪鱼罐头汞含量数值更稳定,D正确。故选ACD。
5. 设矩形的长为 a,宽为 b,其比满足$b:a=\frac{\sqrt{5}-1}{2}\approx0.618$,这种矩形给人以美感,称为黄金矩形。黄金矩形常应用于工艺品设计中。下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:
甲批次:0.598 0.625 0.628 0.595 0.639
乙批次:0.618 0.613 0.592 0.622 0.620
根据上述两个样本来估计两个批次的总体平均数,与标准值 0.618 比较,正确结论是(
A.甲批次的总体平均数与标准值更接近
B.乙批次的总体平均数与标准值更接近
C.两个批次总体平均数与标准值接近程度相同
D.两个批次总体平均数与标准值接近程度不能确定
甲批次:0.598 0.625 0.628 0.595 0.639
乙批次:0.618 0.613 0.592 0.622 0.620
根据上述两个样本来估计两个批次的总体平均数,与标准值 0.618 比较,正确结论是(
A
)A.甲批次的总体平均数与标准值更接近
B.乙批次的总体平均数与标准值更接近
C.两个批次总体平均数与标准值接近程度相同
D.两个批次总体平均数与标准值接近程度不能确定
答案:
5.A 解析:$\overline{x_{甲}}=\frac{0.598 + 0.625 + 0.628 + 0.595 + 0.639}{5}=0.617$,$\overline{x_{乙}}=\frac{0.618 + 0.613 + 0.592 + 0.622 + 0.620}{5}=0.613$,$\therefore \overline{x_{甲}}$与$0.618$更接近。
6. 某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是 96~106,样本数据分组为 96~98,98~100,100~102,102~104,104~106。已知样本中产品净重小于 100 克的个数是 36,则样本中净重大于或等于 98 克并且小于 104 克的产品的个数约是(
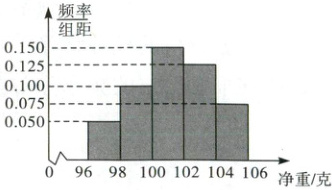
A.90
B.75
C.60
D.45
A
)
A.90
B.75
C.60
D.45
答案:
6.A 解析:产品净重小于$100$克的频率为$(0.050 + 0.100)×2 = 0.300$,已知样本中产品净重小于$100$克的个数是 ,设样本容量为$n$,则$\frac{36}{n}=0.300$,所以$n = 120$。净重大于或等于$98$克并且小于$104$克的产品的频率为$(0.100 + 0.150 + 0.125)×2 = 0.75$,所以样本中净重大于或等于$98$克并且小于$104$克的产品的个数约是$120×0.75 = 90$。故选A。
7. 2022 年 8 月 16 日,航天员的出舱主通道——问天实验舱气闸舱首次亮相。某高中为了解学生对这一新闻的关注度,利用分层抽样的方法从高中三个年级中抽取了 36 人进行问卷调查,其中高一年级抽取了 15 人,高二年级抽取了 12 人,且高三年级共有学生 900 人,则该高中的学生总数为
3600
人。
答案:
7.3600 解析:利用分层抽样的方法从三个年级中抽取了$36$人进行问卷调查,其中高一、高二年级各抽取了$15$人,$12$人,可得高三年级抽取了$9$人,又由高三年级共有$900$名学生,则每个学生被抽到的概率为$p=\frac{9}{900}=\frac{1}{100}$,设该校共有$n$名学生,可得$\frac{36}{n}=\frac{1}{100}$,解得$n = 3600$(人),即该校共有$3600$名学生。故答案为$3600$。
8. 近年来,我国肥胖人群的规模急速增长,肥胖人群有很大的心血管安全隐患。目前,国际上常用身体质量指数(BMI)来衡量人体胖瘦程度以及是否健康,其计算公式是$BMI=\frac{体重(单位:千克)}{身高^{2}(单位:米)}$。我国成人的 BMI 数值标准为:BMI < 18.5 为偏瘦,18.5 ≤ BMI < 24 为正常,24 ≤ BMI < 28 为偏胖,BMI ≥ 28 为肥胖。为了解某公司员工的身体肥胖情况,研究人员从公司员工体检数据中,利用分层抽样得到 15 名员工的 BMI 数据如下:23.5,21.6,30.6,22.1,23.7,20.6,25.5,23.9,20.8,21.5,21.8,18.2,25.2,21.5,19.1。则该组数据的第 70 百分位数为
23.7
。
答案:
8.23.7 解析:$15$名员工的BMI数据由小到大排列为:$18.2$,$19.1$,$20.6$,$20.8$,$21.5$,$21.5$,$21.6$,$21.8$,$22.1$,$23.5$,$23.7$,$23.9$,$25.2$,$25.5$,$30.6$,由$15×70\% = 10.5$,所以该组数据的第$70$百分位数是第$11$个数$23.7$。故答案为$23.7$。
查看更多完整答案,请扫码查看


