《2025年高中同步测控优化训练高中数学必修第二册人教B》

3. 在一定的储存温度范围内，某食品的保鲜时间 $ y $(单位：h)与储存温度 $ x $(单位：$ ° C $)满足函数 $ y = e^{kx + b} $($ e = 2.71828·s $ 为自然对数的底数，$ k,b $ 为常数)，若食品在 $ 0° C $ 时的保鲜时间为 120 h，在 $ 30° C $ 时的保鲜时间为 15 h，则该食品在 $ 20° C $ 时的保鲜时间为30h.

答案： 3.30 解析:由题意可知$\begin{cases}e^b = 120, \\e^{30k + b} = 15,\end{cases}$
$\therefore e^{30k} = \frac{1}{8}$.
$\therefore e^{10k} = \frac{1}{2}$.$\therefore e^{20k + b} = (e^{10k})^2 · e^b = \frac{1}{4} · 120 = 30$.

4. 一个人喝了少量酒后，血液中的酒精含量迅速上升到 0.3 mg/mL，在停止喝酒后，血液中的酒精含量以每小时 25%的速度减少，为了保障交通安全，某地根据《道路交通安全法》规定：驾驶员血液中的酒精含量不得超过 0.09 mg/mL，那么，一个喝了少量酒后的驾驶员，至少经过5h 才能开车.(精确到 1 h，参考数据：$ \lg 3 \approx 0.477 $，$ \lg 4 \approx 0.602 $)

答案： 4.5 解析:设至少经过$x$h才能开车,
由题意得$0.3(1 - 25\%)^x \leq 0.09$,
$\therefore 0.75^x \leq 0.3$,$x \geq \log_{0.75}0.3 \approx 4.2$.

5. 某池塘中野生水葫芦的面积与时间的函数关系的图像如图所示，假设其关系为指数函数，并给出了下列说法：

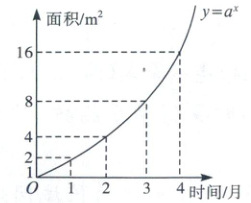
①此指数函数的底数为 2；
②在第 5 个月时，野生水葫芦的面积就会超过 $ 30m^2 $；
③野生水葫芦从 $ 4m^2 $ 蔓延到 $ 12m^2 $ 只需 1.5 个月；
④设野生水葫芦蔓延到 $ 2m^2 $，$ 3m^2 $，$ 6m^2 $ 所需的时间分别为 $ t_1,t_2,t_3 $，则有 $ t_1 + t_2 = t_3 $.
其中正确的说法有①②④.(请把正确说法的序号都填在横线上)

答案：
5.①②④ 解析:该指数函数的解析式为$f(x) = 2^x$,所以①正确;当$x = 5$时,$f(5) = 32 ＞ 30$,所以②正确;由$f(x_1) = 2^{x_1} = 4$和$f(x_2) = 2^{x_2} = 12$,得$x_1 = 2$,$x_2 = \log_2 12 = 2 + \log_2 3$,所以$x_2 - x_1 = \log_2 3 ＞ 1.5$,所以③错误;设$2^{t_1} = 2$,$2^{t_2} = 3$,$2^{t_3} = 6$,则$t_1 = 1$,$t_2 = \log_2 3$,$t_3 = \log_2 6$,则$t_1 + t_2 = 1 + \log_2 3 = \log_2(2 × 3) = \log_2 6 = t_3$,所以④正确.

6. 一片森林原来面积为 $ a $，计划每年砍伐一些树，且每年砍伐面积的百分比相等，当砍伐到面积的一半时，所用时间是 10 年，为保护生态环境，森林面积至少要保留原面积的 $ \frac{1}{4} $，已知到今年为止，森林剩余面积为原来的 $ \frac{\sqrt{2}}{2} $.
（1）求每年砍伐面积的百分比；
（2）到今年为止，该森林已砍伐了多少年；
（3）今后最多还能砍伐多少年.

答案： 6.解:
(1)设每年降低的百分比为$x(0 ＜ x ＜ 1)$,
则$a(1 - x)^{10} = \frac{1}{2}a$,即$(1 - x)^{10} = \frac{1}{2}$,
解得$x = 1 - \left( \frac{1}{2} \right)^{\frac{1}{10}}$.
(2)设经过$m$年剩余面积为原来的$\frac{\sqrt{2}}{2}$,
则$a(1 - x)^m = \frac{\sqrt{2}}{2}a$,即$\left( \frac{1}{2} \right)^{\frac{m}{10}} = \left( \frac{1}{2} \right)^{\frac{1}{2}}$,
$\frac{m}{10} = \frac{1}{2}$,解得$m = 5$.故到今年为止,已砍伐了5年.
(3)设从今年开始,以后砍了$n$年,则$n$年后剩余面积为$\frac{\sqrt{2}}{2}a(1 - x)^n$.
令$\frac{\sqrt{2}}{2}a(1 - x)^n \geq \frac{1}{4}a$,即$(1 - x)^n \geq \frac{\sqrt{2}}{4}$,
$\left( \frac{1}{2} \right)^{\frac{n}{10}} \geq \left( \frac{1}{2} \right)^{\frac{3}{2}}$,$\frac{n}{10} \leq \frac{3}{2}$,解得$n \leq 15$.
故今后最多还能砍伐15年.