《2025年高中同步测控优化训练高中数学必修第二册人教B》

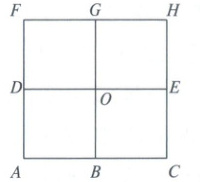
9. 某城市有 8 个商场 $A$，$B$，$C$，$D$，$E$，$F$，$G$，$H$ 和市中心 $O$ 排成如图所示的格局，其中每个小方格为正方形，某人从网格中随机地选择一条最短路径，欲从商场 $A$ 前往商场 $H$，则他经过市中心 $O$ 的概率为$\frac{2}{3}$。

答案： 9. $\frac{2}{3}$解析：此人从商场A前往商场H的所有最短路径有
求概率为$\frac{2}{3}$.

10. 现有 5 根竹竿，它们的长度(单位：$m$)分别为 $2.5$，$2.6$，$2.7$，$2.8$，$2.9$，若从中一次随机抽取 2 根竹竿，则它们的长度恰好相差 $0.3m$ 的概率为$\frac{1}{5}$。

答案： 10. $\frac{1}{5}$解析：从5根竹竿中一次随机抽取2根的可能的基本事件总数为10，它们的长度恰好相差0.3m的基本事件数为2，分别是：2.5和2.8，2.6和2.9，故所求概率为$\frac{1}{5}$.

11. 现共有 6 家企业参与某项工程的竞标，其中 $A$ 企业来自辽宁省，$B$，$C$ 两家企业来自福建省，$D$，$E$，$F$ 三家企业来自河南省。此项工程需要两家企业联合施工，假设每家企业中标的概率相同。
（1）列举所有企业的中标情况；
（2）在中标的企业中，至少有一家来自福建省的概率是多少？

答案： 11. 解：
(1)从这6家企业中选出2家的选法有(A,B)，(A,C)，(A,D)，(A,E)，(A,F)，(B,C)，(B,D)，(B,E)，(B,F)，(C,D)，(C,E)，(C,F)，(D,E)，(D,F)，(E,F)，共有15种，以上就是中标情况.
(2)在中标的企业中，至少有一家来自福建省的选法有(A,B)，(A,C)，(B,C)，(B,D)，(B,E)，(B,F)，(C,D)，(C,E)，(C,F)，共9种.
则“在中标的企业中，至少有一家来自福建省”的概率为$\frac{9}{15}=\frac{3}{5}$.

12. 如图是某校高三（1）班的一次数学知识竞赛成绩的茎叶图（图中仅列出 $[50,60)$、$[90,100)$ 的数据）和频率分布直方图。

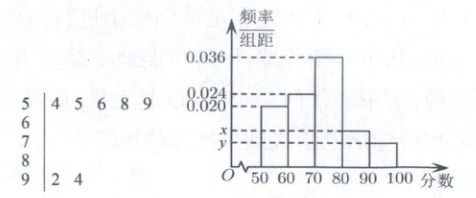
（1）求全班人数以及频率分布直方图中的 $x$，$y$；
（2）估计学生竞赛成绩的平均数和中位数（保留两位小数）。
（3）从得分在 $[80,90)$ 和 $[90,100)$ 中学生中随机抽取两人，求所抽取的两人中至少有一人的得分在区间 $[90,100)$ 的概率是多少？

答案： 12. 解：
(1)分数在$[50,60)$的频率为$0.020×10=0.2$，由茎叶图知，分数在$[50,60)$之间的频数为5，$\therefore$全班人数为$\frac{5}{0.2}=25$（人），分数在$[90,100)$之间的频数为2，则$y=\frac{2}{25}=0.008$，由$10x=1-10×(0.036+0.024+0.020+0.008)$解得$x=0.012$；
(2)平均数为$\bar{x}=55×0.2+65×0.24+75×0.36+85×0.12+95×0.08=71.4$，$\because0.2+0.24+0.36=0.8$，$\therefore$中位数在$[70,80)$内，设中位数为$m$，则$0.2+0.24+(m - 70)×0.036=0.5$，解得$m\approx71.67$，$\therefore$中位数约为71.67.
(3)得分在$[80,90)$内的人数为$25×0.12=3$人，记为A，B，C，得分在$[90,100)$内的人数为2人，记为$a,b$，从这5人中随机抽取2人的所有基本事件为AB，AC，Aa，Ab，BC，Ba，Bb，Ca，Cb，ab，共10个，其中所抽取的两人都在$[80,90)$的基本事件为：AB，AC，BC，共3个，则所抽取的两人中至少有一人的得分在区间$[90,100)$的概率为$P = 1-\frac{3}{10}=\frac{7}{10}$.