《2025年一遍过高中物理必修第二册人教版》

3 [2025黑龙江哈尔滨二模]某同学利用如图甲所示的装置“验证动能定理”，并完成了如下的操作：
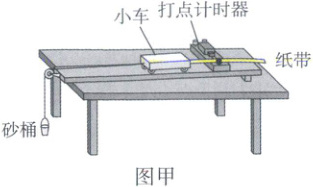
①按如图甲所示的装置组装实验器材，调整滑轮的高度使细线与长木板平行；
②取下砂桶，将长木板的右端适当垫高，纸带穿过打点计时器，开启电源释放小车，直到在纸带上打下一系列均匀的点为止；
③挂上砂桶，并在砂桶中放入适量的砂子，用天平测出砂桶和砂的总质量为$m$，然后将装置由静止释放，重复操作，从其中选择一条点迹比较清晰的纸带，如图乙所示。
已知纸带中相邻两计数点间还有$4$个计时点未画出，计数点间的距离如图乙所示，打点计时器的打点频率$f = 50\ Hz$，重力加速度大小为$g$。
(1)打下计数点$4$时，小车的速度大小$v_4 =$____$m/s$。
(2)若小车的质量为$M$，取打下计数点$1～5$的过程研究，若打下计数点$1$、$5$时小车的速度大小分别为$v_1$和$v_5$，则验证系统动能定理的表达式为____。(用题中所给物理量符号表示)
(3)若砂桶和桶中砂的总质量远小于小车的质量，根据得出的实验数据，描绘出了$v^{2}-W$图像如图丙所示，其中$W = mgh$，则小车的质量$M =$____$kg$。
(4)假设已经完全消除了摩擦力和其他阻力的影响，若砂桶和桶中砂的总质量不满足远小于小车的质量，且$W = mgh$，则从理论上分析，下列各图能正确反映$v^{2}-W$关系的是____；此时若$v^{2}-W$图线直线部分的斜率为$k$，则从理论上分析，可知小车的质量$M =$____。

答案： 3答案
(1)0.192
(2)$mg(h_{5} - h_{1})$=$\frac{1}{2}(m + M)(v_{5}^{2} - v_{1}^{2})$
(3)0.4
(4)A $\frac{2}{k}$-$m$
解析
(1)相邻两计数点间的时间间隔为$T = 5 × \frac{1}{f} =0.1$s，则打下计数点4时，小车的速度大小为$v_{4}$=$\frac{h_{5} - h_{3}}{2T}$=$\frac{(67.2 - 28.8) × 10^{-3}}{2 × 0.1}$m/s = 0.192 m/s。
(2)根据动能定理可知$mg(h_{5} - h_{1})$=$\frac{1}{2}(m + M)(v_{5}^{2} - v_{1}^{2})$。
(3)若砂桶和桶中砂的总质量远小于小车的质量，根据动能定理有W=$\frac{1}{2}Mv^{2}$可得$v^{2}$=$\frac{2}{M}$W，结合题图丙可知$k$=$\frac{2}{M}$=$\frac{0.5}{0.1}kg^{-1}$，可得小车的质量为$M = 0.4 kg$。
(4)若砂桶和桶中砂的总质量不满足远小于小车的质量，根据动能定理有W=$\frac{1}{2}(M + m)v^{2}$，化简可得$v^{2}$=$\frac{2}{M + m}$W，可知选项A正确。由上式可知$k$=$\frac{2}{M + m}$，可得小车的质量为$M$=$\frac{2}{k}$-$m$。

4 某学习兴趣小组用如图所示的装置测量滑块与桌面间的动摩擦因数，图中的力传感器装有无线发射装置，通过无线接收装置与电脑连接，可实时显示力传感器的示数。实验步骤如下：
①用天平测出滑块和传感器的总质量为$m$；
②安装实验装置，在水平桌面上将绳子一端固定在$O$点，另一端与滑块和传感器连接；
③标记滑块在桌面上的位置$P$(图中未标出)，现给滑块一个平行于水平桌面且垂直于绳子方向足够大的初速度$v$，读出此时传感器的示数为$F_1$；
④当滑块再次转动至位置$P$时，读出此时传感器的示数为$F_2$，并截停滑块。
已知重力加速度为$g$，依据上述实验步骤，请回答下面问题：

(1)上述实验中滑块到$O$点的距离$l$是否需要测量____(选填“是”或“否”)。
(2)利用上述实验数据测量的动摩擦因数大小为____(用测出的物理量的字母表示)。
(3)此实验存在较大的误差，测量值会大于真实值的原因可能为____(填写一条即可)。

答案： 4答案
(1)否
(2)$\frac{F_{1} - F_{2}}{4\pi mg}$
(3)滑块受到空气阻力作用
解析
(1)
(2)设滑块初速度为$v_{1}$，转动一圈被截停时的速度为$v_{2}$，由牛顿第二定律可得，在初位置有$F_{1}$=$m\frac{v_{1}^{2}}{l}$，在末位置有$F_{2}$=$m\frac{v_{2}^{2}}{l}$，初位置到末位置由动能定理可知$-\mu mg × 2\pi l$=$\frac{1}{2}mv_{2}^{2}$-$\frac{1}{2}mv_{1}^{2}$，三式联立可得$\mu$=$\frac{F_{1} - F_{2}}{4\pi mg}$，可知不需要测量$l$，即选否。
(3)运动过程中滑块受到空气阻力，会导致$\mu$的测量值偏大。