2025年一遍过高中物理必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年一遍过高中物理必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
1 如图,钢架雪车比赛中,雪车以速率$v$通过截面为四分之一圆弧的弯道,弯道半径为$R$,不计雪车受到的冰面摩擦力。在此情况中( )

A.运动员和雪车所受合外力为零
B.轨道对雪车的弹力为其转弯的向心力
C.若仅增大$v$,则雪车离轨道底部更高
D.若仅增大$R$,则雪车离轨道底部更高

A.运动员和雪车所受合外力为零
B.轨道对雪车的弹力为其转弯的向心力
C.若仅增大$v$,则雪车离轨道底部更高
D.若仅增大$R$,则雪车离轨道底部更高
答案:
1 C 运动员和雪车在圆弧弯道内做圆周运动,处于非平衡状态,所受合力不为零,故A错误;轨道对雪车的弹力与运动员和雪车重力的合力提供其转弯的向心力,故B错误;若仅增大$v$,雪车做圆周运动所需要的向心力变大,轨道对雪车的支持力变大,则雪车离轨道底部更高【提示 设支持力$F_N$与水平面夹角为$\theta$,$F_N = \frac{mg}{\sin \theta}$,$F_N$变大,则$\theta$变小,雪车离轨道底部更高】,故C正确;若仅增大$R$,雪车做圆周运动所需要的向心力变小,轨道对雪车的支持力变小,则雪车离轨道底部更低,故D错误。
2(多选)[2025重庆南坪镇月考]如图所示,内壁光滑的竖直圆桶内,一物块用细绳系着,绳的另一端系于圆桶上表面圆心处。物块贴着圆桶内表面随圆桶一起转动,则( )
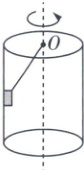
A.绳的拉力可能为零
B.桶壁对物块的弹力不可能为零
C.随着转动的角速度增大,绳的拉力保持不变
D.随着转动的角速度增大,桶壁对物块的弹力一定增大

A.绳的拉力可能为零
B.桶壁对物块的弹力不可能为零
C.随着转动的角速度增大,绳的拉力保持不变
D.随着转动的角速度增大,桶壁对物块的弹力一定增大
答案:
2 CD 由于桶的内壁光滑,不能给物块提供竖直向上的摩擦力去平衡重力,所以绳子的拉力一定不可能等于0,故A错误;对物块受力分析可知绳子拉力沿竖直向上方向的分力与重力的大小相等,若绳子沿水平方向的分力恰好能提供向心力,则桶对物块的弹力可能为零,故B错误;设细绳与竖直方向的夹角为$\theta$,由题图可知绳子与竖直方向的夹角$\theta$不会随桶的角速度的增大而增大,在竖直方向有$T \cos \theta = mg$,所以随着转动的角速度增大,绳子的拉力$T$保持不变,故C正确;在水平方向,根据牛顿第二定律有$T \sin \theta + F_N = m \omega^2 r$,随着转动的角速度增大,拉力$T$保持不变,所以桶壁对物块的弹力一定增大,故D正确。
3 进入冬季后,北方的冰雪运动吸引了许多南方游客。如图为雪地转转游戏,人乘坐雪圈(人和雪圈总质量为$50kg$)绕轴以$2rad/s$的角速度在水平雪地上匀速转动,已知水平杆长为$2m$,离地高为$2m$,绳长为$4m$,且绳与水平杆垂直。则雪圈(含人)( )

A.所受的合外力为零
B.做圆周运动的半径为$2m$
C.线速度大小为$4m/s$
D.所受向心力大小为$800N$

A.所受的合外力为零
B.做圆周运动的半径为$2m$
C.线速度大小为$4m/s$
D.所受向心力大小为$800N$
答案:
3 D 根据几何关系可知,雪圈(含人)做匀速圆周运动的半径为$r = \sqrt{2^2 + (4^2 - 2^2)} m = 4 m$,则线速度大小为$v = \omega r = 2 × 4 m/s = 8 m/s$,雪圈(含人)所受的合外力提供所需的向心力,则有$F_{合} = F_{向} = m \omega^2 r = 50 × 2^2 × 4 N = 800 N$,选项D正确,ABC错误。
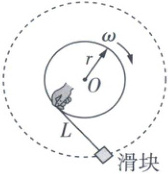
4 [2025江苏苏州中学月考]一个人用手握着长为$L$的轻绳一端,另一端连接一个可视为质点的滑块,当手握的一端在水平桌面上绕$O$点做半径为$r$、角速度为$\omega$的匀速圆周运动时,绳的方向恰好能始终与手的轨迹圆周相切,并使滑块也在同一水平面内做半径更大的匀速圆周运动,如图所示是该运动的俯视图。取重力加速度大小为$g$,则滑块( )
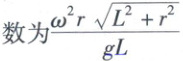
A.角速度小于$\omega$
B.线速度大小为$\omega L$
C.受到的摩擦力方向沿其圆周运动的半径指向$O$点
D.与水平桌面间的动摩擦因数为$\frac{\omega^2r\sqrt{L^2 + r^2}}{gL}$

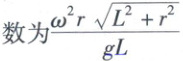
A.角速度小于$\omega$
B.线速度大小为$\omega L$
C.受到的摩擦力方向沿其圆周运动的半径指向$O$点
D.与水平桌面间的动摩擦因数为$\frac{\omega^2r\sqrt{L^2 + r^2}}{gL}$
答案:
4 D 绳的方向恰好能始终与该圆周相切,手运动一周,滑块也运动一周,滑块做匀速圆周运动的角速度也为$\omega$,故A错误;滑块运动半径为$r' = \sqrt{r^2 + L^2}$,所以运动的线速度大小为$v = \omega r' = \omega \sqrt{r^2 + L^2}$,故B错误;滑块受到重力、支持力、绳子的拉力、桌面的滑动摩擦力四个力的作用,其中重力和支持力垂直于水平桌面,拉力沿着绳子,滑动摩擦力方向与滑块的线速度方向相反,与圆周相切,故C错误;设绳子的拉力为$T$,摩擦力与绳子的拉力沿摩擦力反方向的分力等大反向,由几何关系得$\frac{f}{T} = \frac{r}{\sqrt{r^2 + L^2}}$,解得$f = \frac{r T}{\sqrt{r^2 + L^2}}$,设滑块做圆周运动的向心力为$F_{向}$,由几何关系得$\frac{F_{向}}{T} = \frac{L}{\sqrt{r^2 + L^2}}$,又$F_{向} = m \omega^2 \sqrt{r^2 + L^2}$,$f = \mu mg$,解得$\mu = \frac{\omega^2 r \sqrt{L^2 + r^2}}{g L}$,故D正确。
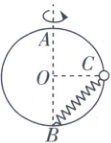
5(多选)[2025黑龙江哈九中月考]如图所示,竖直面内有一半径为$\frac{\sqrt{2}}{2}a$的圆环,可绕直径$AB$所在的竖直轴转动,半径$OC$水平;质量为$m$的小球(可视为质点)套在圆环上,同时有一原长为$\frac{7}{4}a$的轻弹簧一端系于球上,另一端系于$B$点,若圆环以角速度$\omega$匀速转动,小球恰好稳定在圆环上的$C$点,不计一切摩擦,重力加速度大小为$g$,则( )
A.弹簧的劲度系数为$k = \frac{4\sqrt{2}mg}{3a}$
B.弹簧的劲度系数为$k = \frac{\sqrt{2}mg}{a}$
C.圆环受到小球的弹力大小为$mg + \frac{\sqrt{2}}{2}m\omega^2a$
D.圆环受到小球的弹力大小为$\frac{\sqrt{2}}{2}m\omega^2a$

A.弹簧的劲度系数为$k = \frac{4\sqrt{2}mg}{3a}$
B.弹簧的劲度系数为$k = \frac{\sqrt{2}mg}{a}$
C.圆环受到小球的弹力大小为$mg + \frac{\sqrt{2}}{2}m\omega^2a$
D.圆环受到小球的弹力大小为$\frac{\sqrt{2}}{2}m\omega^2a$
答案:
5 AC 由题意可知$BC = a$,弹簧原长为$\frac{7}{4}a$,则小球在$C$点时,弹簧被压缩,则竖直方向上有$k \Delta x \sin 45° = mg$,解得$k = \frac{4 \sqrt{2} mg}{3a}$,选项A正确,B错误;对小球水平方向受力分析,由牛顿第二定律有$F_N - k \Delta x \cos 45° = m \omega^2 · \frac{\sqrt{2}}{2}a$,解得$F_N = mg + \frac{\sqrt{2}}{2} m \omega^2 a$,根据牛顿第三定律可知选项C正确,D错误。
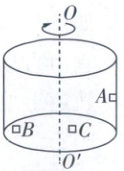
6 [新情境][2025江苏淮阴中学期末考试]如图,半径为$r$的圆筒绕竖直中心轴$OO'$匀速转动,质量为$m$的小物块$A$靠在圆筒的内壁上,质量为$m$的小物块$B$和质量为$\frac{m}{2}$的小物块$C$分别放在筒底距中心轴$\frac{2r}{3}$、$\frac{r}{3}$处,三个小物块均与圆筒保持相对静止。若三个小物块与圆筒接触面的动摩擦因数均为$\mu$,最大静摩擦力等于滑动摩擦力,则$\mu$的最小值为( )
A. $\frac{\sqrt{6}}{3}$
B. $\frac{\sqrt{2}}{2}$
C. $\frac{\sqrt{3}}{6}$
D. $\frac{\sqrt{3}}{2}$
A. $\frac{\sqrt{6}}{3}$
B. $\frac{\sqrt{2}}{2}$
C. $\frac{\sqrt{3}}{6}$
D. $\frac{\sqrt{3}}{2}$

答案:
6 A 对筒底的小物块有$f = M R \omega^2$,又$N = Mg$,故最大静摩擦力$f_m = \mu N \geqslant f$,联立解得$\omega \leqslant \sqrt{\frac{\mu g}{R}}$,因为$R_B > R_A$,可知转速逐渐增大时,$B$先滑动,对小物块$B$有$\omega \leqslant \sqrt{\frac{3 \mu g}{2 r}}$,可得$\mu \geqslant \frac{2 r \omega^2}{3 g}$;对小物块$A$受力分析,有$N' = m r \omega^2$,$f' = mg$,故最大静摩擦力$f_m' = \mu N' \geqslant f'$,联立解得$\mu \geqslant \frac{g}{r \omega^2}$,可得$\mu + \mu \geqslant \frac{2 r \omega^2}{3 g} + \frac{g}{r \omega^2} \geqslant \frac{2 \sqrt{6}}{3}$【提示 对勾函数,当且仅当$\frac{2 r \omega^2}{3 g} = \frac{g}{r \omega^2}$时,等号成立】,可知$\mu$的最小值为$\frac{\sqrt{6}}{3}$,选项A正确。
查看更多完整答案,请扫码查看


