第85页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1. 如图 24-11-6 所示,分别以 $Rt\triangle ABC$ 的三边 $AB$、$BC$、$CA$ 为直径向外作半圆,设直线 $AB$ 左边阴影部分的面积为 $S_{1}$,右边阴影部分的面积和为 $S_{2}$,则(
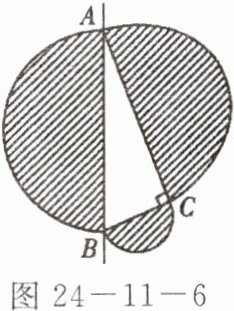
A.$S_{1} = S_{2}$
B.$S_{1} \lt S_{2}$
C.$S_{1} \gt S_{2}$
D.无法确定
A
)
A.$S_{1} = S_{2}$
B.$S_{1} \lt S_{2}$
C.$S_{1} \gt S_{2}$
D.无法确定
答案:
A 点拨:$S_{1}=\frac{1}{2}π\cdot(\frac{AB}{2})^{2}=\frac{πAB^{2}}{8}$,$S_{2}=\frac{1}{2}π(\frac{AC}{2})^{2}+\frac{1}{2}π(\frac{BC}{2})^{2}=\frac{πAC^{2}}{8}+\frac{πBC^{2}}{8}$。因为$△ABC$是直角三角形,所以$AB^{2}=AC^{2}+BC^{2}$,$∴S_{2}=\frac{π}{8}(AC^{2}+BC^{2})=\frac{π}{8}AB^{2}=S_{1}$,故选A。
2. 已知,$AB$ 为半圆的直径,$\overset{\frown}{AB}$长为 $l_{1}$,在半圆内作$\odot O'使之与\overset{\frown}{AB}$、$AB$都相切,$\odot O'$ 的周长为 $l_{2}$,则 $l_{1}$ 与 $l_{2}$ 的关系是(
A.$l_{1} \gt l_{2}$
B.$l_{1} = l_{2}$
C.$l_{1} \geq l_{2}$
D.$l_{1} \lt l_{2}$
C
)A.$l_{1} \gt l_{2}$
B.$l_{1} = l_{2}$
C.$l_{1} \geq l_{2}$
D.$l_{1} \lt l_{2}$
答案:
C
3. 圆心角为 $40^{\circ}$ 的扇形的面积为 $9\pi$,则此扇形所在的圆的半径为
9
。
答案:
9
4. (1) 在$\odot O$ 中,半径是 $30\ cm$,$\overset{\frown}{AB}$ 的长是 $8\pi\ cm$,则$\overset{\frown}{AB}$所对的圆心角是
(2) 在$\odot O$ 中,$108^{\circ}$ 的圆心角所对的弧长是 $12\pi\ cm$,则$\odot O$ 的半径 $R = $
$48^{\circ}$
;(2) 在$\odot O$ 中,$108^{\circ}$ 的圆心角所对的弧长是 $12\pi\ cm$,则$\odot O$ 的半径 $R = $
20
$cm$。
答案:
(1)$48^{\circ}$
(2)20
(1)$48^{\circ}$
(2)20
5. 如图 24-11-7,已知点 $A$、$B$、$C$、$D$ 均在已知圆上,$AD// BC$,$BD$ 平分$\angle ABC$,$\angle BAD = 120^{\circ}$,且四边形 $ABCD$ 的周长为 $15$。求:
(1) 此圆的半径;
(2) 图中阴影部分的面积。
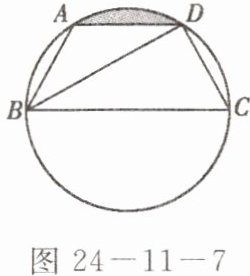
(1) 此圆的半径;
(2) 图中阴影部分的面积。

答案:
解:
(1)$∵AD// BC$,$∠BAD = 120^{\circ}$,$∴∠ABC = 60^{\circ}$。又$∵BD$平分$∠ABC$,$∴∠ABD = ∠DBC = ∠ADB = 30^{\circ}$,$∴\widehat{AB}=\widehat{AD}=\widehat{CD}$,$∠BCD = 60^{\circ}$,$∴AB = AD = DC$,$∠BDC = 90^{\circ}$。在$Rt△BDC$中,$BC$是圆的直径,$BC = 2DC$,$∴BC+\frac{3}{2}BC = 15$,$∴BC = 6$。$∴$此圆的半径为3。
(2)设$BC$的中点为$O$,由
(1)可知$O$即为圆心,连接$OA$,$OD$,过$O$作$OE⊥AD$于$E$。在$Rt△AOE$中,$∠AOE = 30^{\circ}$,$∴OE = \frac{\sqrt{3}}{2}OA = \frac{3\sqrt{3}}{2}$。$∴S_{△AOD}=\frac{1}{2}×3×\frac{3\sqrt{3}}{2}=\frac{9\sqrt{3}}{4}$。$∴S_{阴影}=S_{扇形OAD}-S_{△AOD}=\frac{60×π×3^{2}}{360}-\frac{9\sqrt{3}}{4}=\frac{3π}{2}-\frac{9\sqrt{3}}{4}=\frac{6π - 9\sqrt{3}}{4}$。
(1)$∵AD// BC$,$∠BAD = 120^{\circ}$,$∴∠ABC = 60^{\circ}$。又$∵BD$平分$∠ABC$,$∴∠ABD = ∠DBC = ∠ADB = 30^{\circ}$,$∴\widehat{AB}=\widehat{AD}=\widehat{CD}$,$∠BCD = 60^{\circ}$,$∴AB = AD = DC$,$∠BDC = 90^{\circ}$。在$Rt△BDC$中,$BC$是圆的直径,$BC = 2DC$,$∴BC+\frac{3}{2}BC = 15$,$∴BC = 6$。$∴$此圆的半径为3。
(2)设$BC$的中点为$O$,由
(1)可知$O$即为圆心,连接$OA$,$OD$,过$O$作$OE⊥AD$于$E$。在$Rt△AOE$中,$∠AOE = 30^{\circ}$,$∴OE = \frac{\sqrt{3}}{2}OA = \frac{3\sqrt{3}}{2}$。$∴S_{△AOD}=\frac{1}{2}×3×\frac{3\sqrt{3}}{2}=\frac{9\sqrt{3}}{4}$。$∴S_{阴影}=S_{扇形OAD}-S_{△AOD}=\frac{60×π×3^{2}}{360}-\frac{9\sqrt{3}}{4}=\frac{3π}{2}-\frac{9\sqrt{3}}{4}=\frac{6π - 9\sqrt{3}}{4}$。
(1) 观察与思考:如图 24-11-8①,已知$\odot O$的半径为 $R$(常数),当$\odot O$ 与直线 $AB$ 切于点 $A$ 时,将$\odot O$ 沿直线 $AB$ 滚动(无滑动)一周到点 $B$,则圆心 $O$ 移动的距离是____;

(2) 实验与计算:如图 24-11-8②、③,当$\odot O$ 与边长等于$\odot O$ 周长的三角形或正方形的一边相切时,将$\odot O$ 沿正三角形或正方形周边滚动(无滑动)回到初始位置,分别求出圆心 $O$ 移动的路程;
(3) 探究与推广:一般地,将(2)中的“正三角形或正方形”改为正 $n$ 边形,其他条件和操作要求不变,求圆心 $O$ 移动的路程 $s$ 与 $n$($n$ 为大于或等于 $3$ 的整数)之间的关系。

(2) 实验与计算:如图 24-11-8②、③,当$\odot O$ 与边长等于$\odot O$ 周长的三角形或正方形的一边相切时,将$\odot O$ 沿正三角形或正方形周边滚动(无滑动)回到初始位置,分别求出圆心 $O$ 移动的路程;
(3) 探究与推广:一般地,将(2)中的“正三角形或正方形”改为正 $n$ 边形,其他条件和操作要求不变,求圆心 $O$ 移动的路程 $s$ 与 $n$($n$ 为大于或等于 $3$ 的整数)之间的关系。
答案:
解:
(1)$2πR$
(2)如答图,$\odot O$沿$△ABC$周边滚动时圆心$O$移动线路是$C_{1}→C_{2}→B_{1}→B_{2}→A_{1}→A_{2}→C_{1}$,因为$A_{2}C_{1}+C_{2}B_{1}+B_{2}A_{1}=3×2πR = 6πR$。当$\odot O$滚动到与$AC$切于$C$时,$O$与$C_{1}$重合,所以$C_{1}C⊥AC$。当$\odot O$滚动到与$BC$切于$C$时,$O$与$C_{2}$重合,所以$C_{2}C⊥BC$。因为$∠ACB = 60^{\circ}$,所以$∠C_{1}CC_{2}=120^{\circ}$。所以$\odot O$在三个顶点处三段弧$(\widehat{A_{1}A_{2}},\widehat{B_{1}B_{2}},\widehat{C_{1}C_{2}})$的总长为$3×\frac{120πR}{180}=2πR$,$\odot O$的圆心移动的路程为$6πR + 2πR = 8πR$。当$\odot O$沿正方形的周边滚动时,圆心移动的路程为$4×2πR + 4×\frac{90πR}{180}=10πR$。

(3)从
(2)可知,当$\odot O$沿正$n$边形的周边滚动时,圆心$O$移动的路程为:$s = n\cdot 2πR+\frac{180-\frac{(n - 2)180}{n}}{180}\cdot πR\cdot n=n\cdot 2πR + 2πR = 2(n + 1)πR$。
解:
(1)$2πR$
(2)如答图,$\odot O$沿$△ABC$周边滚动时圆心$O$移动线路是$C_{1}→C_{2}→B_{1}→B_{2}→A_{1}→A_{2}→C_{1}$,因为$A_{2}C_{1}+C_{2}B_{1}+B_{2}A_{1}=3×2πR = 6πR$。当$\odot O$滚动到与$AC$切于$C$时,$O$与$C_{1}$重合,所以$C_{1}C⊥AC$。当$\odot O$滚动到与$BC$切于$C$时,$O$与$C_{2}$重合,所以$C_{2}C⊥BC$。因为$∠ACB = 60^{\circ}$,所以$∠C_{1}CC_{2}=120^{\circ}$。所以$\odot O$在三个顶点处三段弧$(\widehat{A_{1}A_{2}},\widehat{B_{1}B_{2}},\widehat{C_{1}C_{2}})$的总长为$3×\frac{120πR}{180}=2πR$,$\odot O$的圆心移动的路程为$6πR + 2πR = 8πR$。当$\odot O$沿正方形的周边滚动时,圆心移动的路程为$4×2πR + 4×\frac{90πR}{180}=10πR$。

(3)从
(2)可知,当$\odot O$沿正$n$边形的周边滚动时,圆心$O$移动的路程为:$s = n\cdot 2πR+\frac{180-\frac{(n - 2)180}{n}}{180}\cdot πR\cdot n=n\cdot 2πR + 2πR = 2(n + 1)πR$。
查看更多完整答案,请扫码查看


