第78页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
阅读材料:如图 24-8-14①,$\triangle ABC的周长为l$,内切$\odot O的半径为r$,连接$OA$,$OB$,$OC$,$\triangle ABC$被划分为三个小三角形,用$S表示\triangle ABC$的面积.
因为$S = S_{\triangle OAB} + S_{\triangle OBC} + S_{\triangle OCA}$,又因为$S_{\triangle OAB} = \frac{1}{2}AB\cdot r$,$S_{\triangle OBC} = \frac{1}{2}BC\cdot r$,$S_{\triangle OCA} = \frac{1}{2}AC\cdot r$,
所以$S = \frac{1}{2}AB\cdot r + \frac{1}{2}BC\cdot r + \frac{1}{2}AC\cdot r = \frac{1}{2}l\cdot r$,
所以$r = \frac{2S}{l}$.
 (1)理解与应用:利用阅读材料中的结论,计算三边长分别为 5,12,13 的三角形内切圆半径;
(1)理解与应用:利用阅读材料中的结论,计算三边长分别为 5,12,13 的三角形内切圆半径;
(2)类比与推理:若四边形$ABCD$存在内切圆(与各边都相切的圆,如图 24-8-14②)且四边形面积为$S$,各边长分别为$a$,$b$,$c$,$d$,试推导四边形的内切圆半径公式;
(3)拓展与延伸:若一个$n$边形($n$为不小于 3 的整数)存在内切圆,且$n边形面积为S$,各边长分别为$a_1$,$a_2$,$a_3$,…$$,$a_n$,合理猜想其内切圆半径公式(不需说明理由).
因为$S = S_{\triangle OAB} + S_{\triangle OBC} + S_{\triangle OCA}$,又因为$S_{\triangle OAB} = \frac{1}{2}AB\cdot r$,$S_{\triangle OBC} = \frac{1}{2}BC\cdot r$,$S_{\triangle OCA} = \frac{1}{2}AC\cdot r$,
所以$S = \frac{1}{2}AB\cdot r + \frac{1}{2}BC\cdot r + \frac{1}{2}AC\cdot r = \frac{1}{2}l\cdot r$,
所以$r = \frac{2S}{l}$.
 (1)理解与应用:利用阅读材料中的结论,计算三边长分别为 5,12,13 的三角形内切圆半径;
(1)理解与应用:利用阅读材料中的结论,计算三边长分别为 5,12,13 的三角形内切圆半径;(2)类比与推理:若四边形$ABCD$存在内切圆(与各边都相切的圆,如图 24-8-14②)且四边形面积为$S$,各边长分别为$a$,$b$,$c$,$d$,试推导四边形的内切圆半径公式;
(3)拓展与延伸:若一个$n$边形($n$为不小于 3 的整数)存在内切圆,且$n边形面积为S$,各边长分别为$a_1$,$a_2$,$a_3$,…$$,$a_n$,合理猜想其内切圆半径公式(不需说明理由).
答案:
(1)由勾股定理的逆定理可知,三边长分别为5,12,13的三角形是直角三角形,其面积为30,这时$r=\frac{2×30}{5+12+13}=2$.
(2)设四边形ABCD的内切圆的圆心为O,连接OA,OB,OC,OD,并设内切圆的半径为r,依照阅读材料提供的思路,可得:$S=S_{\triangle OAB}+S_{\triangle OBC}+S_{\triangle OCD}+S_{\triangle ODA}=\frac{1}{2}a\cdot r+\frac{1}{2}b\cdot r+\frac{1}{2}c\cdot r+\frac{1}{2}d\cdot r$,所以$r=\frac{2S}{a+b+c+d}$.
(3)猜想:$r=\frac{2S}{a_{1}+a_{2}+\cdots+a_{n}}$.点拨:通过阅读理解,我们学到了推导三角形内切圆半径公式的方法,并把这种方法运用到四边形的内切圆半径公式的推导上,进而推广到存在内切圆的任意多边形中去,体现了从特殊到一般的研究数学问题的方法.本题让我们的观察、分析、类比、猜想、探究等方面能力得到了很好的提高.
(1)由勾股定理的逆定理可知,三边长分别为5,12,13的三角形是直角三角形,其面积为30,这时$r=\frac{2×30}{5+12+13}=2$.
(2)设四边形ABCD的内切圆的圆心为O,连接OA,OB,OC,OD,并设内切圆的半径为r,依照阅读材料提供的思路,可得:$S=S_{\triangle OAB}+S_{\triangle OBC}+S_{\triangle OCD}+S_{\triangle ODA}=\frac{1}{2}a\cdot r+\frac{1}{2}b\cdot r+\frac{1}{2}c\cdot r+\frac{1}{2}d\cdot r$,所以$r=\frac{2S}{a+b+c+d}$.
(3)猜想:$r=\frac{2S}{a_{1}+a_{2}+\cdots+a_{n}}$.点拨:通过阅读理解,我们学到了推导三角形内切圆半径公式的方法,并把这种方法运用到四边形的内切圆半径公式的推导上,进而推广到存在内切圆的任意多边形中去,体现了从特殊到一般的研究数学问题的方法.本题让我们的观察、分析、类比、猜想、探究等方面能力得到了很好的提高.
1. 两圆没有公共点时,两圆一定(
A.相交
B.外离
C.内含
D.外离或内含
D
)A.相交
B.外离
C.内含
D.外离或内含
答案:
D 点拨:两圆没有公共点,则两圆可能是外离,也可能是内含.
2. 如图 24-9-1 所示,7×4 的方格(每个方格的边长为 1 个单位)中,⊙A 的半径为 1,⊙B 的半径为 2,将⊙A 由图示位置向右平移 1 个单位后,⊙A 与静止的⊙B 的位置关系是(
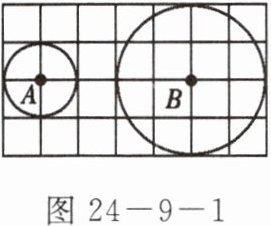
A.内含
B.内切
C.相交
D.外切
D
)
A.内含
B.内切
C.相交
D.外切
答案:
D
3. 已知$⊙O_1 $和$⊙O_2 $的半径分别为 1 和 4,如果两圆的位置关系为相交,那么圆心距$ O_1O_2 $的取值范围在数轴上表示正确的是(
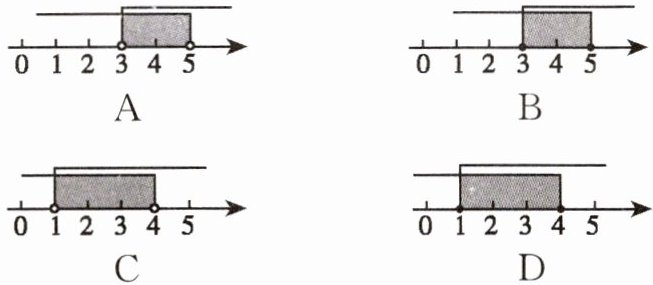
A
)
答案:
A 点拨:相交时,$4-1<O_{1}O_{2}<4+1$,即$3<O_{1}O_{2}<5$.因为取值中不包含3和5两点,所以用空心圆圈表示,所以表示正确的为A.
查看更多完整答案,请扫码查看


