《2025年三维数字课堂九年级数学上册人教版》

1. 如图 24 - 1 - 6,在 Rt△ABC 中,∠C = 90°,AB = 10,若以点 C 为圆心,CB 长为半径的圆恰好经过 AB 的中点 D,则 AC 的长等于(A)

A.5$\sqrt{3}$
B.5
C.5$\sqrt{2}$
D.6

答案： A　点拨:连接CD,则AD=BD=CD=BC=5,易得AC=5$\sqrt{3}$.

2. 如图 24 - 1 - 7,点 A、D、G、M 在半圆 O 上,四边形 ABOC、DEOF、HMNO 均为矩形,设 BC = a,EF = b,NH = c,则下列各式中正确的是(B)

A.a ＞ b ＞ c
B.a = b = c
C.c ＞ a ＞ b
D.b ＞ c ＞ a

答案： B　点拨:由矩形的性质可知OM=NH=c,OA=BC=a,OD=EF=b,又
∵OM=OA=OD,
∴a=b=c.

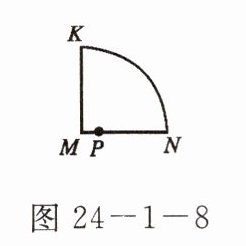
3. 如图 24 - 1 - 8,在圆心角为 90°的扇形 MNK 中,动点 P 从点 M 出发,沿 MN → $\overset{\frown}{NK}$ → KM 运动,最后回到点 M 的位置. 设点 P 运动的路程为 x,P、M 两点之间的距离为 y,其图象可能是(B)

答案： B　点拨:由点P运动的轨迹可知，当点P在$\widehat{NK}$上运动时，y保持不变;又MN=MK，则两端的x的变化量相同，即选项B正确.

4. 一点和⊙O 上的点的最近距离为 4 cm,最远距离为 10 cm,则这个圆的半径是 3cm或7cm.

答案： 3cm或7cm　点拨:此题易出现漏解的现象.其原因是只考虑一种情况，点在圆内或在圆外.在题目没有明确的情况下，点在圆内和圆外两种情况都要考虑.

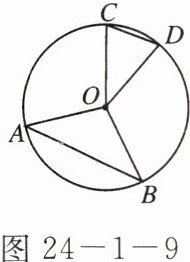
5. 如图 24 - 1 - 9,AB、CD 是⊙O 的两条弦,∠AOB 与∠C 互补,∠COD 与∠A 相等,则∠AOB 的度数是 108°.

答案： 108°　点拨:设∠C=x,则∠AOB=180°-x,∠COD=180°-2x,∠A=$\frac{x}{2}$.由题意，得180°-2x=$\frac{x}{2}$,即x=72°,故∠AOB=108°.

6. 如图 24 - 1 - 10,已知 AB 为⊙O 的直径,半径 OC ⊥ AB,E 为 OB 上一点,弦 AD ⊥ CE 交 OC 于点 F,猜想 OE 与 OF 的数量关系,并说明你的理由.

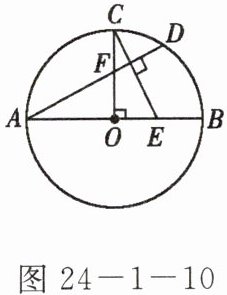
答案： 解:OE=OF.理由如下:
∵OC⊥AB,
∴∠AOF=∠COE=90°.
又
∵AD⊥CE,
∴∠C+∠CEO=∠CEO+∠A=90°.
∴∠C=∠A.又
∵OA=OC,
∴可将△AOF绕点O顺时针旋转90°得到△COE.
∴OE与OF重合,即OE=OF.

如图 24 - 1 - 11,在等腰梯形 ABCD 中,AB // CD. 将△ACD 沿对角线 AC 翻折后,点 D 恰好与边 AB 的中点 M 重合.
(1)点 C 是否在以 AB 为直径的圆上？请说明理由.
(2)当 AB = 4 时,求此梯形的面积.

答案：
解:
(1)点C在以AB为直径的圆上.理由如下:
如答图24−1−2,连接MC,MD.
∵AB//CD,
∴∠DCA=∠BAC;
∵∠DAC=∠BAC,
∴∠DAC=∠DCA,
∴AD=CD.
∵AD=AM,
∴CD=AM,
∴四边形AMCD是平行四边形,
∴MC=AD.同理MD=BC.
∵AD=BC,
∴MC=MD=AD=BC=MA=MB,
∴点C在以AB为直径的圆上.
(2)由
(1)得△AMD是等边三角形,如答图24−1−2,过点D作DE⊥AB于点E,由勾股定理得DE=$\sqrt{2^2-1^2}$=$\sqrt{3}$
∴梯形ABCD的面积=$\frac{1}{2}$×(2+4)×$\sqrt{3}$=3$\sqrt{3}$