《2025年三维数字课堂九年级数学上册人教版》

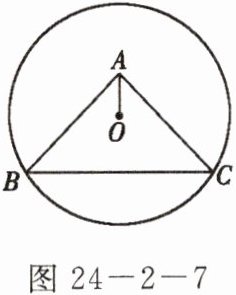
1. 如图 24 - 2 - 7,$\odot O过点B$,$C$,圆心$O在等腰Rt\triangle ABC$的内部,$\angle BAC = 90^{\circ}$,$OA = 1$,$BC = 6$,则$\odot O$的半径为(C)

A.6
B.13
C.$\sqrt{13}$
D.$2\sqrt{13}$

答案： C 点拨:如答图24 - 2 - 1,连接OB、OC,作AD⊥BC于D,
∵△ABC是等腰直角三角形，
∴AD是底边BC的垂直平分线，∠ABC = 45°。
∵OB = OC,
∴点O在AD上，
∴BD = AD = 1/2 BC = 1/2×6 = 3,
∴OD = AD - OA = 3 - 1 = 2。在Rt△OBD中，由勾股定理得OB = √(BD² + OD²) = √(3² + 2²) = √13,故选C。

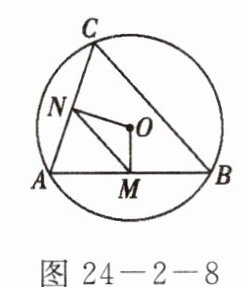
2. 如图 24 - 2 - 8,$AB$,$AC都是\odot O$的弦,$OM\perp AB$,$ON\perp AC$,垂足分别是点$M$,$N$,如果$MN = 3$,那么$BC = $6。

答案： 6 点拨:
∵ON⊥AC,OM⊥AB,
∴AN = CN,AM = BM,
∴BC = 2MN = 2×3 = 6。

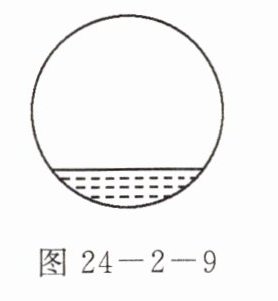
3. 如图 24 - 2 - 9 是一条水平铺设的直径为 2 米的管道横截面,其水面宽 1.6 米,则这条管道中此时水最深为0.4米。

答案： 0.4 点拨:如答图24 - 2 - 2所示,连接AO,过点O作OC⊥AB于点C,交⊙O于点D,因为AB = 1.6米,所以AC = 0.8米，管道横截面直径为2米，所以半径OA = 1米。在Rt△OAC中，根据勾股定理得OC = √(OA² - AC²) = √(1² - 0.8²) = 0.6(米),所以水深CD = OD - OC = 1 - 0.6 = 0.4(米)。

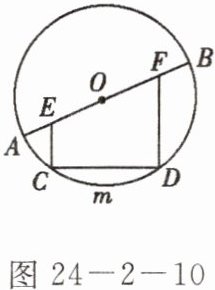
4. 如图 24 - 2 - 10,$\odot O的直径AB = 15$ cm,有一定长为 9 cm 的动弦$CD在\overset{\frown}{AmB}$上滑动(点$C与点A$,点$D与点B$不重合),且$CE\perp CD交AB于E$,$DF\perp CD交AB于F$。
(1)求证：$AE = BF$；
(2)在动弦$CD$滑动过程中,四边形$CDFE$的面积是否发生变化？若变化,请说明理由；若不变,请予以证明并求出这个定值。
]

答案：
(1)证明:过O作OG⊥CD于G,由垂径定理得G为CD中点，又
∵EC⊥CD,DF⊥CD,
∴EC//OG//DF,
∴EO = OF。又
∵AO = OB,
∴AO - OE = OB - OF,即AE = BF。
(2)解:四边形CDFE的面积不发生变化。理由如下:连接OC。由
(1)知CG = 1/2 CD = 9/2 cm,在Rt△OCG中,OG = √(OC² - CG²) = √((15/2)² - (9/2)²) = 6(cm)。
∴S四边形CDFE = OG·CD = 6×9 = 54(cm²),即CD在⌢AB上滑动时,四边形CDFE的面积始终为54 cm²。

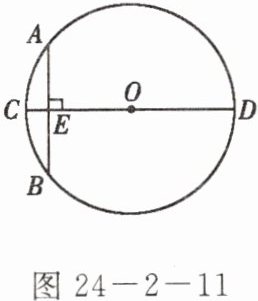
5. 如图 24 - 2 - 11,$CD为\odot O$的直径,弦$AB\perp CD$,垂足为$E$,$CE = 1$,$AB = 10$,求直径$CD$的长。
]

答案： 解:连接OA,设⊙O的半径为R。
∵AB⊥CD,
∴AE = 1/2 AB = 1/2×10 = 5。在Rt△AOE中,OA² = AE² + OE²,即R² = 5² + (R - 1)²,解得R = 13,
∴CD = 2R = 2×13 = 26。

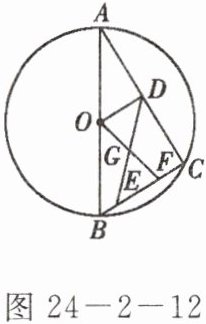
如图 24 - 2 - 12,$AB是\odot O$的直径,$C是\odot O$上一点,过圆心$O作OD\perp AC$,$D$为垂足,$E是BC$上一点,$G是DE$的中点,$OG的延长线交BC于F$。
(1)图中线段$OD$,$BC$所在的直线有怎样的位置关系？写出你的结论,并给出证明过程。
(2)猜想线段$BE$,$EF$,$FC$三者之间有怎样的数量关系。写出你的结论,并给出证明过程。
]

答案： 解:
(1)结论:OD//BC。证明如下:连接OC,
∵OA = OC = OB,
∴∠OAC = ∠OCA,∠OBC = ∠OCB。又
∵∠OAC + ∠OCA + ∠OCB + ∠OBC = 180°,
∴∠OCA + ∠OCB = 90°。
∴∠ACB = 90°,即BC⊥AC。又
∵OD⊥AC,
∴OD//BC。
(2)结论:EF = BE + FC。证明如下:
∵OD⊥AC,
∴AD = DC。又
∵O为AB的中点，
∴OD是△ABC的中位线，
∴BC = 2OD。在△ODG和△FEG中，
∵DG = EG,∠GOD = ∠GFE,∠ODG = ∠FEG,
∴△ODG≌△FEG,
∴OD = EF,BE + EF + FC = BC = 2OD = 2EF,
∴EF = BE + FC。