第77页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1. 如图 24-8-8,$\triangle ABC的内切圆\odot O与各边相切于点D$、$E$、$F$,且$\angle FOD = \angle EOD = 135^{\circ}$,则$\triangle ABC$一定不是(
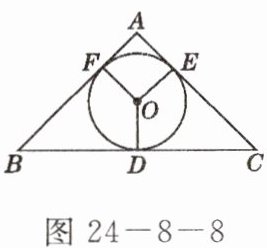
A.等腰三角形
B.等边三角形
C.直角三角形
D.等腰直角三角形
]
B
)
A.等腰三角形
B.等边三角形
C.直角三角形
D.等腰直角三角形
]
答案:
B
2. 如图 24-8-9,正三角形内切圆的半径为 1,则正三角形的边长为(
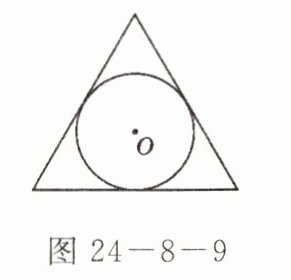
A.2
B.$2\sqrt{3}$
C.$\sqrt{3}$
D.3
B
)
A.2
B.$2\sqrt{3}$
C.$\sqrt{3}$
D.3
答案:
B 点拨:利用圆外一点和圆心的连线平分过这点引的圆的两条切线的夹角,得出一个锐角是30°的直角三角形,利用勾股定理再进一步求解.
3. 如图 24-8-10,以正方形$ABCD的BC边为直径作半圆O$,过点$D作直线切半圆于点F$,交$AB于点E$,则$\triangle ADE和直角梯形EBCD$的周长之比为(
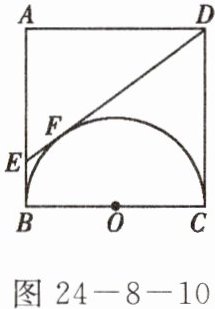
A.$3:4$
B.$4:5$
C.$5:6$
D.$6:7$
]
D
)
A.$3:4$
B.$4:5$
C.$5:6$
D.$6:7$
]
答案:
D 点拨:设正方形的边长为a,BE=x.由切线长定理知BE=EF=x,CD=DF=a,在Rt△AED中,AE=a−x,AD=a,DE=a+x.由勾股定理可知$DE^{2}=AE^{2}+AD^{2}$,所以$(a+x)^{2}=(a−x)^{2}+a^{2}$,解得$x=\frac{1}{4}a$.所以△DAE的周长为AD+AE+DE=3a.直角梯形EBCD的周长为BE+DE+CD+BC=$\frac{7}{2}a$.所以它们的比值为$3a:\frac{7}{2}a=6:7$.
4. 如图 24-8-11,AC是$\odot O$的直径$,\angle ACB = 60^{\circ},$连接AB,过A,B两点分别作$\odot O$的切线,两切线交于点P. 若已知$\odot O$的半径为 1,则$\triangle PAB$的周长为
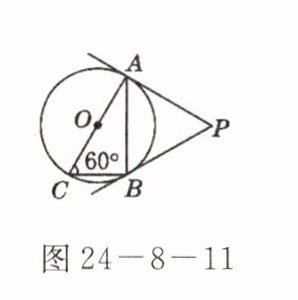
$3\sqrt{3}$
.
答案:
$3\sqrt{3}$ 点拨:在Rt△ABC中求出AB的长,再证明△PAB是等边三角形,由此求出△PAB的周长.此题虽是填空题,但涉及的知识点较多.
5. 为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用有一个锐角为$30^{\circ}$的三角板和一把刻度尺,按如图 24-8-12 所示的方法得到相关数据,进而可求得铁环的半径. 若三角板与圆相切且测得$PA = 5$ cm,求铁环的半径.
]
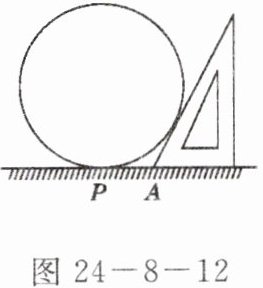
]

答案:
解:设铁环的圆心为O,三角板与$\odot O$相切于点B,连接OP,OA(如答图24−8−2).

答图24−8−2
因为AP,AB是$\odot O$的切线,所以OP⊥PA,∠PAO=$\frac{1}{2}$∠PAB=60°,所以∠POA=30°,所以OA=2PA=10cm,所以$OP=\sqrt{OA^{2}-PA^{2}}=\sqrt{100-25}=5\sqrt{3}(cm)$.所以铁环的半径为$5\sqrt{3}\ cm$.点拨:本题以生活问题为背景,考查了我们对切线长定理的理解和运用.此类题关键是将实际问题转化为数学问题,体现了数学的转化思想.
解:设铁环的圆心为O,三角板与$\odot O$相切于点B,连接OP,OA(如答图24−8−2).

答图24−8−2
因为AP,AB是$\odot O$的切线,所以OP⊥PA,∠PAO=$\frac{1}{2}$∠PAB=60°,所以∠POA=30°,所以OA=2PA=10cm,所以$OP=\sqrt{OA^{2}-PA^{2}}=\sqrt{100-25}=5\sqrt{3}(cm)$.所以铁环的半径为$5\sqrt{3}\ cm$.点拨:本题以生活问题为背景,考查了我们对切线长定理的理解和运用.此类题关键是将实际问题转化为数学问题,体现了数学的转化思想.
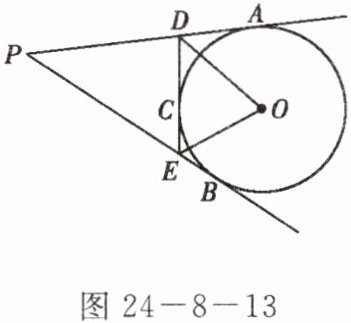
6. 如图 24-8-13,$P是\odot O$外一点,$PA$,$PB分别和\odot O切于A$,$B$,$PA = PB = 4$ cm,$\angle APB = 40^{\circ}$,$C是\overset{\frown}{AB}$上任意一点,过$C作\odot O$的切线,分别交$PA$,$PB于D$,$E$. 求:
(1)$\triangle PDE$的周长;
(2)$\angle DOE$的度数.
]
(1)$\triangle PDE$的周长;
(2)$\angle DOE$的度数.
]

答案:
(1)如答图24−8−3,

连接OA,OB,OC.
∵PA,PB,DE分别是$\odot O$的切线,A,B,C为切点,
∴OA⊥PA,OB⊥PB,OC⊥DE,
∴DA=DC,EB=EC,
∴DE=DC+CE=DA+EB,
∴△PDE的周长为PD+PE+DE=PD+PE+DA+EB=PA+PB=4+4=8(cm).
(2)
∵PA,PB为$\odot O$的切线,
∴∠PAO=∠PBO=90°,在四边形APBO中,∠AOB=180°−∠P=140°,
∵DA,DC为$\odot O$的切线,
∴DA=DC,∠ADO=∠CDO,又
∵DO=DO,
∴△ADO≌△CDO,
∴∠1=∠2.同理∠3=∠4,
∴∠DOE=∠2+∠3=$\frac{1}{2}$∠AOB=$\frac{1}{2}×140^{\circ}=70^{\circ}$.
(1)如答图24−8−3,

连接OA,OB,OC.
∵PA,PB,DE分别是$\odot O$的切线,A,B,C为切点,
∴OA⊥PA,OB⊥PB,OC⊥DE,
∴DA=DC,EB=EC,
∴DE=DC+CE=DA+EB,
∴△PDE的周长为PD+PE+DE=PD+PE+DA+EB=PA+PB=4+4=8(cm).
(2)
∵PA,PB为$\odot O$的切线,
∴∠PAO=∠PBO=90°,在四边形APBO中,∠AOB=180°−∠P=140°,
∵DA,DC为$\odot O$的切线,
∴DA=DC,∠ADO=∠CDO,又
∵DO=DO,
∴△ADO≌△CDO,
∴∠1=∠2.同理∠3=∠4,
∴∠DOE=∠2+∠3=$\frac{1}{2}$∠AOB=$\frac{1}{2}×140^{\circ}=70^{\circ}$.
查看更多完整答案,请扫码查看


