《2025年三维数字课堂九年级数学上册人教版》

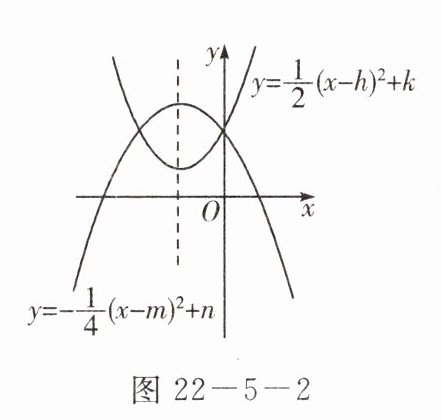
4. 如图 $ 22 - 5 - 2 $,在平面直角坐标系中,有两条位置确定的抛物线,它们的对称轴相同,表达式中的 $ h $,$ k $,$ m $,$ n $ 都是常数,则下列关系不正确的是(D)


A.$ h ＜ 0 $,$ k ＞ 0 $
B.$ m ＜ 0 $,$ n ＞ 0 $
C.$ h = m $
D.$ k = n $

答案： D　点拨:根据二次函数解析式确定两抛物线的顶点坐标分别为(h,k)，(m,n)，对称轴都是直线x=m(或x=h),即m=h,由题图知h＜0,k＞0,m＜0,n＞0,因为点(h,k)在点(m,n)的下方，所以k=n不正确.故选D.

5. 若 $ AB // x $ 轴,且与抛物线 $ y = 3(x + 2)^2 + k $ 交于 $ A(-3,n) $、$ B $ 两点,则点 $ B $ 的横坐标为 −1。

答案： −1　点拨:AB//x轴，
∴点A和点B关于抛物线的对称轴对称，设点B的横坐标为m,
∵二次函数y=3(x+2)²+k的图象的对称轴为直线x=−2,
∴m−(−2)=−2−(−3),
∴m=−1.

6. 如图 $ 22 - 5 - 3 $,抛物线 $ y_1 = -x^2 + 2 $ 向右平移 $ 1 $ 个单位得到抛物线 $ y_2 $,回答下列问题：
(1) 抛物线 $ y_2 $ 的顶点坐标为 (1,2)；
(2) 阴影部分的面积 $ S = $ 2；
(3) 若再将抛物线 $ y_2 $ 绕原点 $ O $ 旋转 $ 180° $ 得到抛物线 $ y_3 $,则抛物线 $ y_3 $ 的开口方向 向上,顶点坐标为 (−1,−2)。

答案：
(1)(1,2)　
(2)2　
(3)向上　(−1,−2)
点拨:
(1)
∵y1=−x²+2的顶点是(0,2)，
∴抛物线y1向右平移1个单位后顶点坐标为(1,2).
(2)阴影部分的面积通过用割补法可知正好是一个长为2，宽为1的矩形面积.
(3)
∵将抛物线y2绕原点O旋转180°得到抛物线y3，
∴抛物线y3与抛物线y2关于原点对称.
∴抛物线y3的开口向上，顶点坐标为(−1,−2).

7. 已知函数 $ y = -2(x - 3)^2 + 6 $。
(1) 写出函数图象的开口方向、顶点坐标、对称轴；
(2) 求出函数图象与 $ x $ 轴的交点坐标；
(3) 当 $ x $ 为何值时,$ y $ 随 $ x $ 的增大而增大？
(4) 当 $ x $ 为何值时,函数 $ y $ 有最大值或最小值？并求出函数的最值。

答案：
(1)开口向下，对称轴为x=3，顶点坐标为(3,6).
(2)令y=0,即−2(x−3)²+6=0,解得x=±$\sqrt{3}$+3.
∴函数图象与x轴的交点坐标为($\sqrt{3}$+3,0)和(−$\sqrt{3}$+3,0).
(3)当x＜3时,y随x的增大而增大.
(4)当x=3时，函数有最大值，最大值为6.点拨:本题综合考查了y=a(x−h)²+k的图象与性质.特别注意图象与x轴的交点坐标，即要求出y=0时x的值，需解一元二次方程

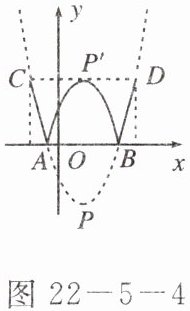
8. 如图 $ 22 - 5 - 4 $,抛物线 $ y = a(x - 1)^2 + c $ 与 $ x $ 轴交于点 $ A(1 - \sqrt{3},0) $ 和点 $ B $,将抛物线沿 $ x $ 轴向上翻折,顶点 $ P $ 落在点 $ P'(1,3) $ 处。求原抛物线的解析式。

答案： 解:
∵点P与点P'(1,3)关于x轴对称，
∴P点坐标为(1,−3).
∵抛物线y=a(x−1)²+c过点A(1−$\sqrt{3}$,0),顶点是P(1,−3),
∴$\begin{cases} a(1-\sqrt{3}-1)^2+c=0 \\ a(1-1)^2+c=-3 \end{cases}$解得$\begin{cases} a=1 \\ c=-3 \end{cases}$，则抛物线的解析式为y=(x−1)²−3,即y=x²−2x−2.

如图 $ 22 - 5 - 5 $,已知抛物线 $ y = -(x - m)^2 + 1 $ 与 $ x $ 轴的交点为 $ A $,$ B $($ B $ 在 $ A $ 的右边),与 $ y $ 轴的交点为 $ C $。
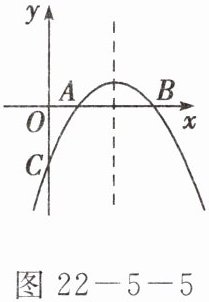
(1) 写出 $ m = 1 $ 时,与抛物线有关的三个正确结论；
(2) 当点 $ B $ 在原点的右边,点 $ C $ 在原点的下方时,是否存在 $ \triangle BOC $ 为等腰三角形的情形？若存在,求出 $ m $ 的值；若不存在,请说明理由；
(3) 请你提出一个对任意的 $ m $ 值都能成立的正确命题。

答案：
(1)当m=1时，抛物线的解析式为y=−(x−1)²+1=−x²+2x,正确的结论有很多，如:①抛物线的解析式为y=−x²+2x;②抛物线的开口向下;③顶点坐标为(1,1);④抛物线经过原点;⑤与x轴的另一个交点的坐标是(2,0);⑥对称轴为直线x=1;⑦当x=1时，函数取得最大值y=1;等等.
(2)存在.当y=0时,−(x−m)²+1=0,即(x−m)²=1,
∴x1=m−1,x2=m+1.
∵点B在点A的右边,
∴点A坐标为(m−1,0),点B坐标为(m+1,0).
∴OB=m+1.
∵当x=0时,y=−m²+1,点C在原点下方，
∴OC=m²−1.当m²−1=m+1时,m²−m−2=0,
∴m1=2,m2=−1(不符合题意，舍去),
∴存在△BOC为等腰三角形的情形，此时m=2.
(3)可写出的命题有:①对任意的m,抛物线y=−(x−m)²+1的顶点都在直线y=1上;②对任意的m,抛物线y=−(x−m)²+1与x轴的两个交点间的距离是一个定值;③对任意的m,抛物线y=−(x−m)²+1与x轴两个交点的横坐标之差的绝对值是2.点拨:在解答探究开放型问题时，首先应理解问题中的条件和图形中的信息，往往在几个问题的探究过程中都是由浅入深、循序渐进，同时需要从已给资料或已经解答的问题(及其过程)中寻求解答后面问题的思想和方法，对开放型问题的探究要注意探究所深入的层次和结论的普遍性意义以及结论的一般性.