第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1. 矩形$ABCD$中,$AB = 8$,$BC = 3\sqrt{5}$,点$P在边AB$上,且$BP = 3AP$,如果$\odot P是以点P$为圆心,$PD$为半径的圆,那么下列判断正确的是(
A.点$B$、$C均在\odot P$外
B.点$B在\odot P$外、点$C在\odot P$内
C.点$B在\odot P$内、点$C在\odot P$外
D.点$B$、$C均在\odot P$内
C
)A.点$B$、$C均在\odot P$外
B.点$B在\odot P$外、点$C在\odot P$内
C.点$B在\odot P$内、点$C在\odot P$外
D.点$B$、$C均在\odot P$内
答案:
C 点拨:易得PB=6,PC=9,⊙P的半径为7,则点B在⊙P内,点C在⊙P外
2. 如果点$O为\triangle ABC$的外心,$\angle BOC = 70^{\circ}$,那么$\angle BAC$等于(
A.$35^{\circ}$
B.$110^{\circ}$
C.$145^{\circ}$
D.$35^{\circ}或145^{\circ}$
D
)A.$35^{\circ}$
B.$110^{\circ}$
C.$145^{\circ}$
D.$35^{\circ}或145^{\circ}$
答案:
D 点拨:∠BAC为△ABC外接圆的圆周角,又
∵∠BOC=70°,
∴∠BAC=35°或145°.
∵∠BOC=70°,
∴∠BAC=35°或145°.
3. 如图$24 - 5 - 4$,在$\mathrm{Rt}\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = 6$,$AB = 10$,$CD是斜边AB$上的中线,以$AC为直径作\odot O$,设线段$CD的中点为P$,则点$P与\odot O$的位置关系是(
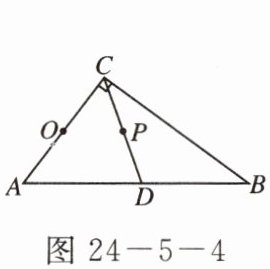
A.点$P在\odot O$内
B.点$P在\odot O$上
C.点$P在\odot O$外
D.无法确定
A
)
A.点$P在\odot O$内
B.点$P在\odot O$上
C.点$P在\odot O$外
D.无法确定
答案:
A 点拨:连接OP,则OP为△ACD的中位线,OP=1/2AD=1/4AB=5/2.由已知易得⊙O的半径为3,故点P在⊙O内.
4. 如图$24 - 5 - 5$,$\odot O是正三角形ABC$的外接圆,点$P在劣弧AB$上,$\angle ABP = 22^{\circ}$,则$\angle BCP$的度数为
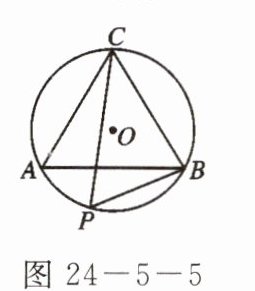
38°
。
答案:
38°
5. 用反证法证明命题“$\triangle ABC$中至少有两个锐角”时,第一步假设为
△ABC中只有一个锐角.
。
答案:
△ABC中只有一个锐角.
6. 如图$24 - 5 - 6$,$\triangle ABC是\odot O$的内接三角形,点$D是\overgroup{BC}$的中点,已知$\angle AOB = 98^{\circ}$,$\angle COB = 120^{\circ}$,则$\angle ABD$的度数是
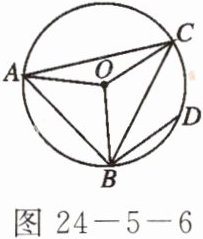
101°
。
答案:
101° 点拨:由∠AOB=98°,∠COB=120°,得∠AOC=142°,
∴∠ABC=71°.
∵D是⌢BC的中点,
∴∠CBD=1/2∠BAC=1/4∠BOC=30°,
∴∠ABD=∠ABC+∠CBD=101°.
∴∠ABC=71°.
∵D是⌢BC的中点,
∴∠CBD=1/2∠BAC=1/4∠BOC=30°,
∴∠ABD=∠ABC+∠CBD=101°.
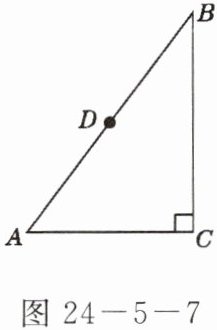
7. 如图$24 - 5 - 7$,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$AB = 5\mathrm{cm}$,$BC = 4\mathrm{cm}$,以$A$为圆心,$3\mathrm{cm}$为半径作圆,试判断:
(1)点$C与\odot A$的位置关系;
(2)点$B与\odot A$的位置关系;
(3)$AB的中点D与\odot A$的位置关系。
(1)点$C与\odot A$的位置关系;
(2)点$B与\odot A$的位置关系;
(3)$AB的中点D与\odot A$的位置关系。

答案:
解:
(1)由勾股定理,得AC=√(5²-4²)=3(cm).当以点A为圆心,3cm为半径作圆时,有r=d,故点C在⊙A上.
(2)AB=5cm,有d>r,故点B在⊙A外.
(3)因为点D是AB的中点,AB=5cm,所以AD=2.5cm,d<r,故AB的中点D在⊙A内.点拨:判断点与圆的位置关系时,只需确定点与圆心的距离及圆的半径,然后进行比较即可.
(1)由勾股定理,得AC=√(5²-4²)=3(cm).当以点A为圆心,3cm为半径作圆时,有r=d,故点C在⊙A上.
(2)AB=5cm,有d>r,故点B在⊙A外.
(3)因为点D是AB的中点,AB=5cm,所以AD=2.5cm,d<r,故AB的中点D在⊙A内.点拨:判断点与圆的位置关系时,只需确定点与圆心的距离及圆的半径,然后进行比较即可.
如图$24 - 5 - 8$,已知梯形$ABCD$中,$AB// CD$,$AD = BC$,$AB = 48$,$CD = 30$,高为$27$,求作一个圆经过$A$,$B$,$C$,$D$四点,写出作法并求出这个圆的半径。
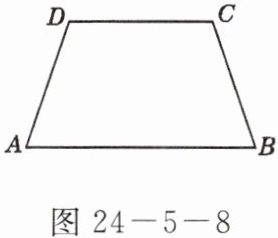

答案:
解:分别作DC,AD的垂直平分线l,m,交点为O,则O为△ADC的外接圆圆心(如答图24-5-2).设l与CD,AB分别交于E,F,连接OA,OB,OC,OD.因为四边形ABCD为等腰梯形,所以l为其对称轴,所以OB=OA.因为OC=OD,OD=OA,OA=OB,所以O为等腰梯形ABCD的外接圆的圆心.以O为圆心,OA为半径作圆,即为所求的圆.设OE=x,则OF=27-x.因为OC=OB,所以√(15²+x²)=√((27-x)²+24²),解得x=20.所以OC=√(15²+20²)=25,即这个圆的半径为25.点拨:要求作一个圆经过A,B,C,D四个点,应该先选三个点确定一个圆,然后证明第四个点也在圆上即可.再利用勾股定理列方程可求得圆的半径.
查看更多完整答案,请扫码查看


