第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1. 如图 23 - 4 所示的图形旋转一定角度后能与自身重合,则旋转的角度可能是(
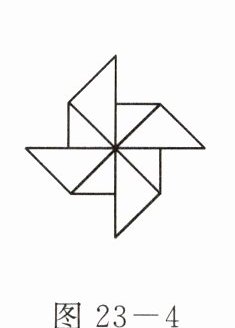
A.30°
B.60°
C.90°
D.120°
C
)
A.30°
B.60°
C.90°
D.120°
答案:
C
2. 若点 P(3,- n),Q(m,- 4)关于原点对称,则 P、Q 两点间的距离是(
A.5
B.10
C.20
D.10$\sqrt{2}$
B
)A.5
B.10
C.20
D.10$\sqrt{2}$
答案:
B
3. 如图 23 - 5 所示,Rt△ABC 的边 BC 绕点 C 旋转到 CE 的位置,则下列说法正确的是(

A.点 B 与点 D 为对应点,且∠ACD = ∠BCE
B.∠ACB = ∠BCE
C.AB = DE
D.线段 AB 与线段 CE 是对应线段
C
)
A.点 B 与点 D 为对应点,且∠ACD = ∠BCE
B.∠ACB = ∠BCE
C.AB = DE
D.线段 AB 与线段 CE 是对应线段
答案:
C
4. 如图 23 - 6 所示,面积为$ 12 cm^2 $的△ABC 沿 BC 方向平移至△DEF 的位置,平移的距离是边 BC 长的 2 倍,则图中的四边形 ACED 的面积为(
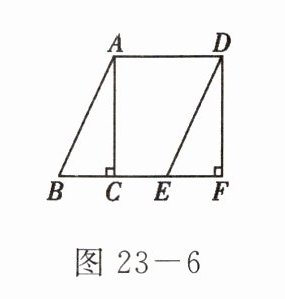
$A. 24 cm^2$
$B. 36 cm^2$
$C. 48 cm^2$
D. 无法确定
B
)
$A. 24 cm^2$
$B. 36 cm^2$
$C. 48 cm^2$
D. 无法确定
答案:
B
5. 如图 23 - 7,△ABC 绕点 B 逆时针方向旋转到△EBD 的位置,若∠A = 15°,∠C = 10°,E,B,C 在同一直线上,则旋转角为

15
度.
答案:
15
6. 如图 23 - 8 所示,△ABC 以点 A 为旋转中心,按逆时针方向旋转 90°得到△AB′C′,则△ABB′是
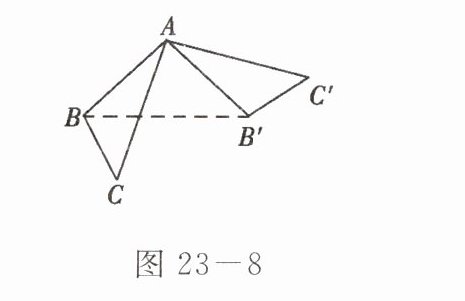
等腰直角
三角形.
答案:
等腰直角
7. 如图 23 - 9 所示,线段 AB,CD 互相平分于点 O,过 O 作 EF 交 AC 于 E,交 BD 于 F,则这个图形是中心对称图形,对称中心是 O,图形中的对应点是

A与B,C与D,E与F,O与O
,对应线段是OA与OB,OC与OD,OE与OF,AC与BD,AE与BF,CE与DF
,对应三角形是△AEO与△BFO,△CEO与△DFO,△ACO与△BDO
.
答案:
对应点是A与B,C与D,E与F,O与O;对应线段是OA与OB,OC与OD,OE与OF,AC与BD,AE与BF,CE与DF;对应三角形是△AEO与△BFO,△CEO与△DFO,△ACO与△BDO。
8. 如图 23 - 10 所示,已知面积为 1 的正方形 ABCD 的对角线相交于点 O,过点 O 作任一条直线分别交 AD,BC 于点 E,F,则阴影部分的面积是
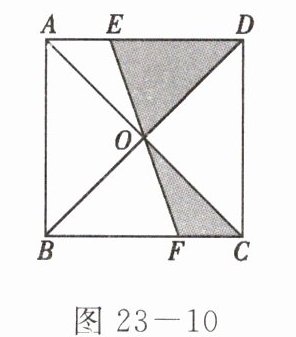
1/4
.
答案:
1/4
9. 在如图 23 - 11 所示的方格纸中,每个小方格都是边长为 1 个单位的正方形,△ABC 的三个顶点都在格点上(每个小方格的顶点叫格点).
(1)画出△ABC 绕点 O 顺时针旋转 90°后的$△A_1B_1C_1;$
(2)求点 A 旋转到$ A_1 $所经过的路线长.
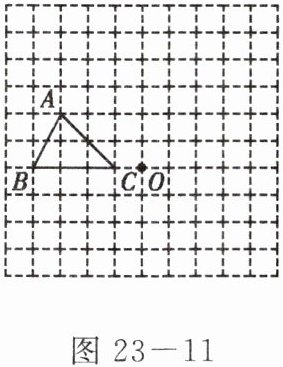
(1)画出△ABC 绕点 O 顺时针旋转 90°后的$△A_1B_1C_1;$
(2)求点 A 旋转到$ A_1 $所经过的路线长.

答案:
(1) 按题意画出$\triangle A_1B_1C_1$,如图所示(图略,需在方格纸上绕点$O$顺时针旋转$90°$后的三角形)。
(2) 点$A$旋转到$A_1$所经过的路线长为$\frac{\sqrt{10}}{2} \pi$(或$\frac{\sqrt{10} \pi}{2}$)。
(1) 按题意画出$\triangle A_1B_1C_1$,如图所示(图略,需在方格纸上绕点$O$顺时针旋转$90°$后的三角形)。
(2) 点$A$旋转到$A_1$所经过的路线长为$\frac{\sqrt{10}}{2} \pi$(或$\frac{\sqrt{10} \pi}{2}$)。
查看更多完整答案,请扫码查看


