《2025年三维数字课堂九年级数学上册人教版》

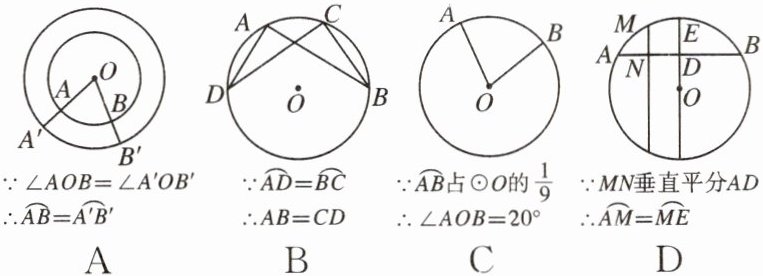
1. 观察下列选项中的各图及相应推理,其中正确的是(B)

答案： B

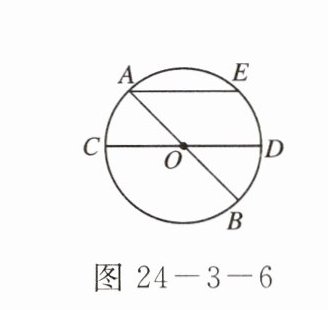
2. 如图 24 - 3 - 6,已知 AB、CD 是$\odot O$的两条直径,且$∠AOC = 50^{\circ}$,过点 A 作$AE // CD交\odot O$于点 E,则$\overset{\frown}{AE}$的度数为(D)

A.$65^{\circ}$
B.$70^{\circ}$
C.$75^{\circ}$
D.$80^{\circ}$

答案： D　点拨:连接OE.
∵AE//CD,
∴$\widehat{AC}=\widehat{DE}$.又
∵∠AOC=50°,
∴∠EOD=50°,
∴∠AOE=80°.

3. 在$\odot O$中,弦 AB 与半径 OC 互相垂直平分,则弦 AB 所对的圆心角为120°

答案： 120°

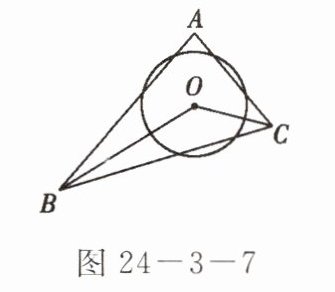
4. 如图 24 - 3 - 7,在$\triangle ABC$中,$∠A = 80^{\circ}$,且$\odot O$在三边上截得的弦长相等,则$∠BOC$的度数为______.

130°

答案： 130°　点拨:过O作OM⊥AB,ON⊥AC,OP⊥BC,垂足分别为M,N,P.
∵∠A=80°,
∴∠ABC+∠ACB=180°−∠A=100°.又
∵OM=ON=OP,
∴O是∠ABC和∠ACB平分线的交点.
∴∠BOC=180°−$\frac{1}{2}$(∠ABC+∠ACB)=180°−$\frac{1}{2}$×100°=130°.

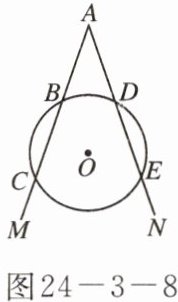
5. 如图 24 - 3 - 8,射线 AM 交$\odot O$于点 B、C,射线 AN 交$\odot O$于点 D、E,且$\overset{\frown}{BC} = \overset{\frown}{DE}$. 求证：$AC = AE$.

答案： 证明:如答图24−3−2,连接AO,过圆心O作AM、AN的垂线段OF、OG.在⊙O中，
∵$\widehat{BC}=\widehat{DE}$,
∴BC=DE,
∴OF=OG.
∴Rt△AFO≌Rt△AGO,
∴AF=AG.
∵OF⊥BC,OG⊥DE,
∴FC=$\frac{1}{2}$BC,GE=$\frac{1}{2}$DE,
∴FC=GE,
∴AC=AE.

6. 如图 24 - 3 - 9,A 点是半圆上一个三等分点,B 点是$\overset{\frown}{AN}$的中点,P 是直径 MN 上一动点,$\odot O$的半径为 1,则$AP + BP$的最小值为多少？

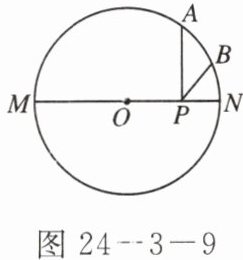
答案： 解:作点A关于MN的对称点A',根据圆的对称性，则A'必在⊙O上.连接BA'交MN于点P,连接PA,则PA十PB最小，此时PA+PB=PA'+PB=A'B.连接OA、OA'、OB.
∵$\widehat{AN}=\frac{1}{3}\widehat{MN}$,
∴∠A'ON=∠AON=60°.
∵$\widehat{AB}=\widehat{BN}$,
∴∠BON=$\frac{1}{2}$∠AON=30°,
∴∠A'OB=90°,
∴A'B=$\sqrt{OA'^2+OB^2}=\sqrt{1^2+1^2}=\sqrt{2}$即AP+BP的最小值是$\sqrt{2}$

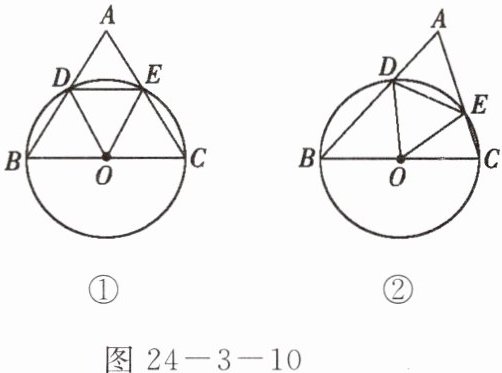
如图 24 - 3 - 10①,在$\triangle ABC$中,$∠A = 60^{\circ}$,以 BC 为直径的$\odot O$分别交 AB,AC 于 D,E.
(1) 若$AB = AC$,求证：$\triangle DOE$是等边三角形；
(2) 如图 24 - 3 - 10②所示,$AB \neq AC$,则(1)中的结论是否成立？如果成立,请给出证明；如果不成立,请说明理由.

答案：
(1)证明:
∵∠A=60°,AB=AC,
∴△ABC是等边三角形，
∴∠DBO=60°.又
∵OB=OD,
∴△BOD是等边三角形，
∴∠BOD=60°.同理∠COE=60°,
∴∠DOE=180°−∠BOD−∠COE=180°−60°−60°=60°,且OD=OE,
∴△DOE是等边三角形.
(2)解:△DOE仍然是等边三角形.理由如下:
∵BO=DO,
∴∠B=∠BDO,
∴∠BOD=180°−2∠B,同理∠EOC=180°−2∠C,
∴∠DOE=180°−(∠BOD+∠EOC)=180°−[(180°−2∠B)+(180°−2∠C)]=180°−[360°−2(∠B+∠C)]=2(∠B+∠C)−180°=2(180°−∠A)−180°=2×(180°−60°)−180°=60°,且OD=OE,
∴△DOE是等边三角形.