《2025年三维数字课堂九年级数学上册人教版》

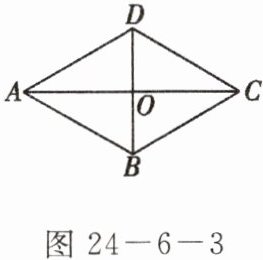
6. 如图$24-6-3$,菱形$ABCD的对角线AC$,$BD交于点O$,且$AC= 6$,$BD= 2\sqrt{3}$,以$O$为圆心,$1.5$为半径作圆。试说明$\odot O与AD$相切。

答案：
解:如答图24−6−2,过O作OE⊥AD,垂足为E.在菱形ABCD中,AC=6,BD=2√3,BD与AC垂直且平分，所以AO=3，DO=√3.所以AD=√(3²+(√3)²)=2√3.由三角形的面积,得OE·AD=OA·OD,所以OE=(OA·OD)/AD=(3×√3)/(2√3)=1.5.所以EO=r=1.5.所以⊙O与AD相切.点拨:判断一个圆与直线相切，我们可以从圆心到直线的距离是否等于圆的半径入手进行分析、判断.

7. 如图$24-6-4$,$\odot O的半径OC= 10$cm,直线$l\perp CO$,垂足为$H$,交$\odot O于A$、$B$两点,$AB= 16$cm,直线$l平移多少厘米时能与\odot O$相切？

答案： 解:连接OA,延长CO交⊙O于D,
∵l⊥OC,
∴OC平分AB,
∴AH=8cm.在Rt△AHO中,OH=√(AO² - AH²)=√(10²−8²)=6(cm).
∴CH=4cm,DH=16cm.
∴直线AB向左平移4cm或向右平移16cm时与⊙O相切.

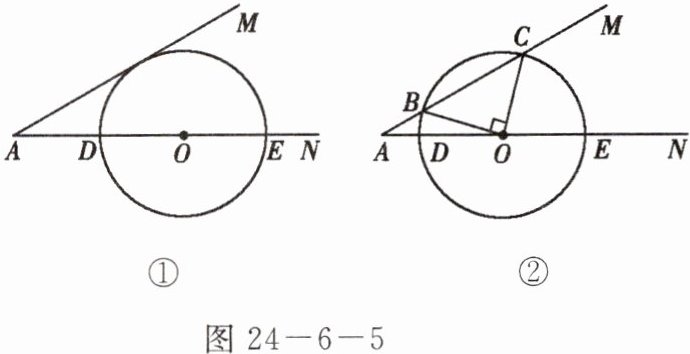
已知$\angle MAN= 30^{\circ}$,$O为AN$上一点,以$O$为圆心,$2为半径作\odot O$,交$AN于D$,$E$两点,设$AD= x$。
(1)如图$24-6-5$①所示,当$x$为何值时,$\odot O与AM$相切？
(2)如图$24-6-5$②所示,当$x$为何值时,$\odot O与AM相交于B$,$C$两点,且$\angle BOC= 90^{\circ}$？

答案：
解:
(1)假设⊙O与AM相切于点F,如答图24−6−3①所示，连接OF,则OF=2.又
∵在Rt△OAF中,∠A=30°,
∴OA=2OF=2×2=4,
∴x=AD=OA - OD=4 - 2=2,即x=2时，⊙O与AM相切.
(2)如答图24−6−3②所示,过O作OF⊥BC,垂足为F,
∵OB=OC,且∠BOC=90°,
∴△BOC为等腰直角三角形，
∴OF=BF=CF=(1/2)BC.
∵BC=√(OB² + OC²)=√(2²+2²)=2√2
∴OF=(1/2)BC=√2又
∵在Rt△AOF中,∠OAF=30°,
∴AO=2OF,
∴x + 2=2√2，
∴x=2√2 - 2,
∴当x=2√2 - 2时，⊙O与AM相交于B,C两点,且∠BOC=90°.