《2025年三维数字课堂九年级数学上册人教版》

1. 如果点$A(-2,b)和点B(a,1)$关于坐标原点对称,那么$a$,$b$的值分别是(D)
A.$-2$,$1$
B.$2$,$1$
C.$-2$,$-1$
D.$2$,$-1$

答案： D

2. 矩形$ABCD中的顶点A$、$B$、$C$、$D$按顺时针方向排列,若在平面直角坐标系内,$B$、$D两点对应的坐标分别是(2,0)$,$(0,0)$,且$A$、$C两点关于x$轴对称,则$C$点对应的坐标是((1,−1))
A.$(1,1)$
B.$(1,-1)$
C.$(1,-2)$
D.$(\sqrt{2},-\sqrt{2})$

答案： B　点拨:由矩形对角线互相平分且相等可知AC=2,且过BD的中点(1,0),又
∵A、C两点关于x轴对称，则易得C的坐标为(1,−1).

3. 在图$23 - 4 - 1$所示的方格纸中,每个小正方形的边长为$1$,如果以$MN所在的直线为y$轴,以小正方形的边长为单位长度建立平面直角坐标系,使$A点与B$点关于原点对称,则这时$C$点的坐标是(B)


A.$(1,3)$
B.$(2,-1)$
C.$(2,1)$
D.$(3,1)$

答案： B　点拨:由MN所在直线为y轴可知，点C横坐标为2;又A点与B点关于原点对称，则点C到x轴的距离为1,且在x轴下方，故C点的坐标为(2，−1).

4. 已知$A(3x - 1,2y)和B(2x,3y - 1)$是坐标平面上的两点,若$A$、$B$两点关于原点对称,则点$A$的坐标为$\left(-\dfrac{2}{5},\dfrac{2}{5}\right)$。

答案： $\left(-\dfrac{2}{5},\dfrac{2}{5}\right)$ 点拨:
∵A、B关于原点对称，
∴$\begin{cases} 3x-1+2x=0, \\ 2y+3y-1=0, \end{cases}$解得$\begin{cases} x=\dfrac{1}{5}, \\ y=\dfrac{1}{5}, \end{cases}$
∴点A的坐标为$\left(-\dfrac{2}{5},\dfrac{2}{5}\right).$

5. (1)已知点$P(a - 1,a^{2} - 9)在x$轴的负半轴上,则$P$点关于原点对称的点的坐标为(4,0)；
(2)已知点$A与点B(1,-6)关于y$轴对称,则点$A关于原点的对称点C$的坐标为(1,6)；
(3)若点$P(-1 - 2a,2a - 4)$关于原点对称的点在第一象限内,则整数$a$的值是0或1。

答案：
(1)(4,0)　
(2)(1,6)　
(3)0或1

6. 在图$23 - 4 - 2$所示的编号为①②③④的四个三角形中,关于$y$轴对称的两个三角形的编号为①②,关于坐标原点$O$对称的两个三角形的编号为______①③。
]

答案： ①②　①③

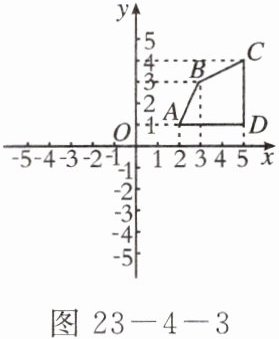
7. 如图$23 - 4 - 3$所示,在平面直角坐标系中,四边形$ABCD和四边形EFGH关于坐标原点O$对称,请利用关于原点对称的点的特征作出四边形$EFGH$。
]

答案：
解:作法如下:
　　　　　　
　由答图23−4−1可知:A(2,1),B(3,3),C(5,4),D(5,1).
(1)A(2,1)关于原点对称的点的坐标是E(−2,−1),在平面直角坐标系中描出;
(2)照
(1)的作法，画出点B、C、D分别关于原点对称的点F、G、H的位置;
(3)顺次连接E、F、G、H即可(如答图23-4−1).

8. 如图$23 - 4 - 4$所示,已知$A(3,1)$、$B(2,2)$、$C(1,-1)$,利用关于原点对称的点的坐标特点,作出与$\triangle ABC$关于原点对称的图形。
]

答案：
解:点P(x,y)关于原点的对称点为$P_1(-x,-y)$,因此$\triangle ABC$的三个顶点A(3,1)、B(2,2)、C(1,−1)关于原点的对称点分别为$A_1(-3,-1)$、$B_1(-2,-2)$、$C_1(-1,1)$,依次连接$A_1B_1$、$B_1C_1$、$C_1A_1$,就可得到$\triangle ABC$关于原点对称的$\triangle A_1B_1C_1$(如答图23−4−2).