《2025年三维数字课堂九年级数学上册人教版》

6. 如图 $ 22 - 4 - 1 $,在 $ \mathrm { Rt } \triangle O A B $ 中,$ \angle O A B = 90 ^ { \circ } $,$ O $ 为坐标原点,边 $ O A $ 在 $ x $ 轴上,$ O A = A B = 1 $ 个单位长度,把 $ \mathrm { Rt } \triangle O A B $ 沿 $ x $ 轴正方向平移 $ 1 $ 个单位长度后得到 $ \triangle A A _ { 1 } B _ { 1 } $。
(1)求以 $ A $ 为顶点,且经过点 $ B _ { 1 } $ 的抛物线的解析式；
(2)若(1)中的抛物线与 $ O B $ 交于点 $ C $,与 $ y $ 轴交于点 $ D $,求点 $ D $、$ C $ 的坐标。

答案： 解:
(1)由题意可知,A(1,0),A₁(2,0),B₁(2,1).设以A为顶点的抛物线的解析式为y=a(x−1)².
∵此抛物线过点B₁(2,1),
∴1=a(2−1)²,
∴a=1,
∴所求抛物线的解析式为y=(x−1)².
(2)
∵当x=0时,y=(0−1)²=1,
∴D点坐标为(0,1).由题意知OB在第一象限内两坐标轴夹角的平分线上，故可设C(m,m),代入y=(x−1)²,得m=(m−1)²,解得m₁=$\frac{3−\sqrt{5}}{2}$＜1,m₂=$\frac{3+\sqrt{5}}{2}$＞1(舍去).故C点坐标为($\frac{3−\sqrt{5}}{2}$,$\frac{3−\sqrt{5}}{2}$).

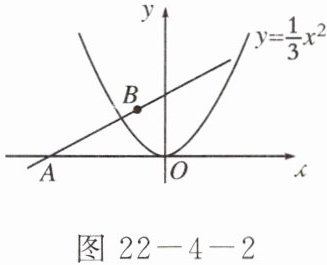
如图 $ 22 - 4 - 2 $,直线 $ y = \frac { \sqrt { 3 } } { 3 } x + b $ 经过点 $ B ( - \sqrt { 3 }, 2 ) $,且与 $ x $ 轴交于点 $ A $,将抛物线 $ y = \frac { 1 } { 3 } x ^ { 2 } $ 沿 $ x $ 轴作左右平移,记平移后的抛物线为 $ C $,其顶点为 $ P $。
(1)求 $ \angle B A O $ 的度数；
(2)抛物线 $ C $ 与 $ y $ 轴交于点 $ E $,与直线 $ A B $ 交于两点,其中一个交点为 $ F $,当线段 $ E F // x $ 轴时,求平移后的抛物线 $ C $ 对应的函数关系式；
(3)在抛物线 $ y = \frac { 1 } { 3 } x ^ { 2 } $ 平移过程中,将 $ \triangle P A B $ 沿直线 $ A B $ 翻折得到 $ \triangle D A B $,点 $ D $ 能否落在抛物线 $ C $ 上？如能,求出此时抛物线 $ C $ 顶点 $ P $ 的坐标；如不能,说明理由。

答案： 解:
(1)由点B在直线AB上，求得b=3,
∴直线AB为y=$\frac{\sqrt{3}}{3}$x+3,
∴A(−3$\sqrt{3}$,0),即OA=3$\sqrt{3}$.如答图，作BH⊥x轴，垂足为H，则BH=2,OH=$\sqrt{3}$,AH=2$\sqrt{3}$,
∴AB=$\sqrt{AH^{2}+BH^{2}}$=4.在Rt△ABH中,AB=2BH,
∴∠BAO=30°.
(2)设抛物线C的顶点为P(t,0),则抛物线的关系式为C:y=$\frac{1}{3}$(x−t)²,
∴E(0,$\frac{1}{3}$t²).
∵EF//x轴,
∴点E、F关于抛物线C的对称轴对称,
∴F(2t,$\frac{1}{3}$t²).
∵点F在直线AB上,
∴$\frac{1}{3}$t²=$\frac{\sqrt{3}}{3}$⋅2t+3,解得t₁=−$\sqrt{3}$,t₂=3$\sqrt{3}$.
∴抛物线C为y=$\frac{1}{3}$(x+$\sqrt{3}$)²或y=$\frac{1}{3}$(x−3$\sqrt{3}$)².
(3)假设点D能落在抛物线C上，不妨设此时抛物线顶点为P(t,0),则抛物线的关系式为C:y=$\frac{1}{3}$(x−t)²,AP=3$\sqrt{3}$+t.连接DP,作DM⊥x轴，垂足为M.由已知,得△PAB≌△DAB.又∠BAO=30°,
∴△PAD为等边三角形,PM=AM=$\frac{1}{2}$(3$\sqrt{3}$+t).
∵DM=$\sqrt{3}$AM,
∴DM=$\frac{1}{2}$(9+$\sqrt{3}$t),OM=PM−OP=$\frac{1}{2}$(3$\sqrt{3}$+t)−t=$\frac{1}{2}$(3$\sqrt{3}$−t),
∴M(−$\frac{1}{2}$(3$\sqrt{3}$−t),0),D(−$\frac{1}{2}$(3$\sqrt{3}$−t),$\frac{1}{2}$(9+$\sqrt{3}$t)).
∵点D落在抛物线C上,
∴$\frac{1}{2}$(9+$\sqrt{3}$t)=$\frac{1}{3}$[−$\frac{1}{2}$(3$\sqrt{3}$−t)−t]²,即t²=27,
∴t=±3$\sqrt{3}$.当t=−3$\sqrt{3}$时,点P(−3$\sqrt{3}$,0),点P与点A重合,不能构成三角形,不符合题意,舍去.
∴点P的坐标为(3$\sqrt{3}$,0).
∴当点D落在抛物线C上时,顶点P的坐标为(3$\sqrt{3}$,0).