第74页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1. 下列直线是圆的切线的是(
A.与圆有公共点的直线
B.圆心到该直线的距离等于圆的半径
C.垂直于圆的半径的直线
D.过圆的半径外端的直线
B
)A.与圆有公共点的直线
B.圆心到该直线的距离等于圆的半径
C.垂直于圆的半径的直线
D.过圆的半径外端的直线
答案:
B
2. 圆的切线(
A.垂直于半径
B.平行于半径
C.垂直于经过切点的半径
D.以上都不对
C
)A.垂直于半径
B.平行于半径
C.垂直于经过切点的半径
D.以上都不对
答案:
C
3. 如图24-7-1所示,AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,还需补充一个条件,则补充的条件不正确的是(

A.DE= DO
B.AB= AC
C.CD= DB
D.AC//OD
A
)
A.DE= DO
B.AB= AC
C.CD= DB
D.AC//OD
答案:
A 点拨:由于D是圆上一点,所以要说明DE是切线,只需证明OD⊥DE即可.又因为DE⊥AC,所以当AC//OD时,可得OD⊥DE.因为当CD=DB时,即D为BC的中点,而O为AB的中点,所以OD//AC.在当AB=AC时,连接AD,因为AB是直径,所以AD⊥BC,所以CD=DB,因此B,C,D选项均可以说明DE是☉O的切线.
4. 如图24-7-2所示,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠A= 25°,则∠D等于(
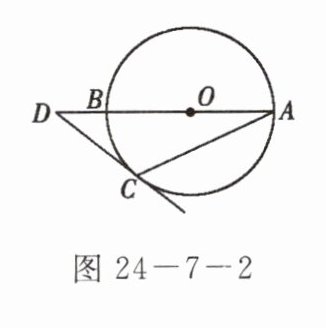
A.20°
B.30°
C.40°
D.50°
C
)
A.20°
B.30°
C.40°
D.50°
答案:
C 点拨:连接OC,由OA=OC得∠OCA=∠A=25°,再利用三角形外角的性质得∠DOC=∠A+∠OCA=50°,由切线性质得∠DCO=90°,
∴∠D=90°−50°=40°.
∴∠D=90°−50°=40°.
5. 如图24-7-3,已知PA是⊙O的切线,A是切点,PC是过圆心的一条割线,点B,C是它与⊙O的交点,且PA= 8,PB= 4,则⊙O的半径为

6
。
答案:
6 点拨:连接OA,构造直角三角形,利用勾股定理列方程.在几何图形中求线段的长,常采用代数方法解决几何问题.
6. 如图24-7-4所示,在△ABC中,∠B= 60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点P,CP交⊙O于点D。
(1)求证:AP= AC;
(2)若AC= 3,求PC的长。
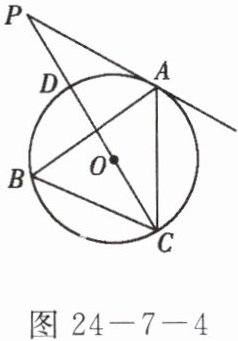
(1)求证:AP= AC;
(2)若AC= 3,求PC的长。

答案:
(1)证明:连接AO,则AO⊥PA,
∵∠B=60°,
∴∠AOC=2∠B=120°,
∴∠AOP=60°,
∴∠P=30°.又
∵OA=OC,
∴∠ACP=30°,
∴∠P=∠ACP,
∴AP=AC.
(2)解:在Rt△PAO中,∠P=30°,PA=3,
∴PO=2OA,
∴PO=2√3,CO=OA=√3,
∴PC=PO+OC=2√3+√3=3√3.
(1)证明:连接AO,则AO⊥PA,
∵∠B=60°,
∴∠AOC=2∠B=120°,
∴∠AOP=60°,
∴∠P=30°.又
∵OA=OC,
∴∠ACP=30°,
∴∠P=∠ACP,
∴AP=AC.
(2)解:在Rt△PAO中,∠P=30°,PA=3,
∴PO=2OA,
∴PO=2√3,CO=OA=√3,
∴PC=PO+OC=2√3+√3=3√3.
1. 如图24-7-5,若⊙O的直径AB与弦AC的夹角为30°,切线CD与AB的延长线交于点D,且⊙O的半径为2,则CD的长为(
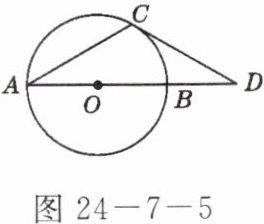
A.2√{3}
B.4√{3}
C.2
D.4
A
)
A.2√{3}
B.4√{3}
C.2
D.4
答案:
A 点拨:连接OC,利用三角形外角与内角的关系得出∠COD=60°,再进一步在Rt△OCD中求CD的长.
2.如图24一7一6,在平面直角坐标系中,点A在第一象限,⊙A与ェ轴相切于点B,与у轴交于C(0,1),D(O,4)两点.则点A 的坐标是()

$A. ( \dfrac {3}{2}, \dfrac {5}{2} )$
$B. ( \dfrac {3}{2},2 )$
$C. ( 2, \dfrac {5}{2} )$
$D. ( \dfrac {5}{2}, \dfrac {3}{2} )$

$A. ( \dfrac {3}{2}, \dfrac {5}{2} )$
$B. ( \dfrac {3}{2},2 )$
$C. ( 2, \dfrac {5}{2} )$
$D. ( \dfrac {5}{2}, \dfrac {3}{2} )$
答案:
C
查看更多完整答案,请扫码查看


