《2025年三维数字课堂九年级数学上册人教版》

5. 若方程 $x^{2}+kx + 9 = 0$ 有两个相等的实数根,则 $k = $±6。

答案： ±6

6. 若 $x = 1$ 是一元二次方程 $(m + 1)x^{2}-m^{2}x - 2m - 1 = 0$ 的一个根,则 $m = $0。

答案： 0 点拨:将x=1代入方程得m+1-m²-2m-1=0,即m(m+1)=0.又
∵m+1≠0,
∴m=0.

7. 已知一元二次方程 $x^{2}-6x - 5 = 0$ 的两根为 $a$、$b$,则 $\frac{1}{a}+\frac{1}{b}$ 的值是-6/5。

答案： -6/5 点拨:1/a + 1/b = (a+b)/ab = 6/(-5) = -6/5.

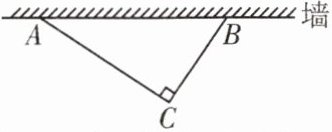
8. 一个小区用篱笆围成一个直角三角形花坛,花坛的斜边利用足够长的墙,两条直角边所用的篱笆长之和恰好为 $21$ 米,围成的花坛如图所示,其中 $\angle ACB = 90^{\circ}$。若所修的直角三角形花坛面积是 $54$ 平方米,则直角三角形的斜边 $AB$ 的长为15米。

答案： 15 点拨:设直角三角形的直角边AC的长为x米,则直角边BC的长为(21-x)米.依题意,得1/2 x·(21-x)=54,整理得x²-21x+108=0,解得x₁=9,x₂=12.当x=9时,21-x=12;当x=12时,21-x=9.在Rt△ABC中,∠ACB=90°,
∴AB=√(AC²+BC²)=√(9²+12²)=15(米).

9. 解下列方程：
(1) $2x^{2}+3x - 1 = 0$；
(2) $7x(2 - x)= 3(x - 2)$；
(3) $9x^{2}-6x - 2 = 0$。

答案：
(1)x=(-3±√(3²+4×2))/(2×2)=(-3±√17)/4,
∴x₁=(-3+√17)/4,x₂=(-3-√17)/4.
(2)7x(2-x)+3(2-x)=0,(2-x)(7x+3)=0,2-x=0或7x+3=0,
∴x₁=2,x₂=-3/7.
(3)(3x-1)²=3,3x-1=±√3,
∴x₁=(1+√3)/3,x₂=(1-√3)/3.

10. 已知关于 $x$ 的一元二次方程 $x^{2}-6x - k^{2}= 0$($k$ 为常数)。
(1)求证：方程有两个不相等的实数根；
(2)设 $x_{1}$,$x_{2}$ 为方程的两个实数根,且 $x_{1}+2x_{2}= 14$,试求出方程的两个实数根和 $k$ 的值。

答案：
(1)
∵b²-4ac=(-6)²-4×1×(-k²)=36+4k²＞0,
∴方程有两个不相等的实数根.
(2)
∵x₁+x₂=-b/a=-(-6)/1=6,又
∵x₁+2x₂=14,
∴可列方程组{x₁+x₂=6,x₁+2x₂=14,解得{x₁=-2,x₂=8.将x₁和x₂代入x₁x₂=c/a,得-2×8=-k²/1,解得k=±4.

11. 某班家委会为每位学生准备了便携式免洗抑菌洗手液。去市场购买时发现：当购买量不超过 $100$ 瓶时,免洗抑菌洗手液的单价为 $8$ 元；超过 $100$ 瓶时,每增加 $10$ 瓶,单价就降低 $0.2$ 元,但最低价格不能低于每瓶 $5$ 元。设家委会共买了 $x$ 瓶免洗抑菌洗手液。
(1)当 $x = 80$ 时,每瓶洗手液的价格是8元；当 $x = 150$ 时,每瓶洗手液的价格是7元；
(2)若家委会购买洗手液共花费 $1200$ 元,则一共购买了多少瓶洗手液？
解：①当0≤x≤100时，8×100=800＜1200（舍去）。
②∵(8-(x-100)/10×0.2)=5，解得x=250，
∴当100＜x≤250时，x(8-(x-100)/10×0.2)=1200，
整理得：x²-500x+60000=0，
解得x₁=200，x₂=300（舍去）。
③当x＞250时，1200÷5=240（舍去）。
答：一共购买了200瓶洗手液。

答案：
(1)8 7 点拨:
∵80＜100,
∴每瓶洗手液的价格是8元.当x=150时,每瓶洗手液的价格是8-(150-100)÷10×0.2=8-1=7(元).解:
(2)①0≤x≤100时,8×100=800＜1200(舍去).②
∵(8-(x-100)/10×0.2)=5,解得x=250,
∴当100＜x≤250时,x(8-(x-100)/10×0.2)=1200.解得x₁=200,x₂=300(舍去),③当x＞250时,1200÷5=240(舍去).答:一共购买了200瓶洗手液.