《2025年三维数字课堂九年级数学上册人教版》

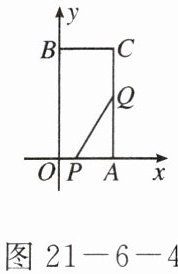
7. 如图21-6-4,在直角坐标系中,四边形$OACB$为矩形,$C$点的坐标为(3,6),若点$P从点O沿OA向点A$以1cm/s的速度运动,点$Q从点A沿AC$以2cm/s的速度运动,如果$P$、$Q分别从O$、$A$同时出发,问：
(1)经过多长时间$\triangle PAQ的面积为2cm^{2}$？
(2)$\triangle PAQ的面积能否达到3cm^{2}$？

答案： 解:
(1)设t s时,$S_{\triangle PAQ}=2cm^{2}$,则$\frac {1}{2}(3-t)\cdot 2t=2$.即$t^{2}-3t+2=0$,解得$t_{1}=1,t_{2}=2.$
(2)设x s时,$S_{\triangle PAQ}=3cm^{2}$,则$\frac {1}{2}(3-x)\cdot 2x=3$.即$x^{2}-3x+3=0$,此时方程无实数根.所以$S_{\triangle PAQ}$不能达到$3cm^{2}.$

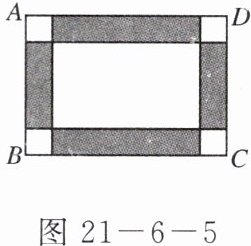
8. 学校计划用地砖铺设教学楼前矩形广场的地面$ABCD$,已知矩形广场地面的长为100米,宽为80米.图案设计如图21-6-5,广场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,阴影部分铺绿色地砖,其余部分铺白色地砖.
(1)要使铺白色地砖的面积为5200平方米,那么矩形广场四角的小正方形的边长为多少米？
(2)如果铺白色地砖的费用为每平方米30元,铺绿色地砖的费用为每平方米20元,当矩形广场四角小正方形的边长为多少米时,铺广场地面的总费用最少？最少费用是多少？

答案： 解:
(1)设矩形广场四角的小正方形的边长为x米,根据题意,得$4x^{2}+(100-2x)(80-2x)=5200$,整理,得$x^{2}-45x+350=0$.解得$x_{1}=35,x_{2}=10$,经检验,$x_{1}=35,x_{2}=10$均符合题意.答:要使铺白色地砖的面积为5200平方米,那么矩形广场四角的小正方形的边长为35米或10米.
(2)设铺矩形广场地面的总费用为y元,广场四角的小正方形的边长为x米,则$y=30×[4x^{2}+(100-2x)(80-2x)]+20×[2x(100-2x)+2x(80-2x)]$.即$y=80x^{2}-3600x+240000$,配方,得$y=80(x-22.5)^{2}+199500$.当x=22.5时,y的值最小,最小值为199500.答:当矩形广场四角的小正方形的边长为22.5米时,铺广场地面的总费用最少,最少费用是199500元.

两个村民一共带了100个鸡蛋去市集,两人所带鸡蛋数不同,但是,卖的钱数一样.第一个村民对第二个村民说：“如果你的鸡蛋给我,我可以卖得45元.”第二个村民答道：“如果你的鸡蛋给我,我只能卖得20元.”问：这两个村民各有多少个鸡蛋？都卖了多少元？

答案： 解:设第一个村民有x个鸡蛋,则第二个村民有(100-x)个鸡蛋.第一个村民卖出的单价为$\frac {45}{100-x}$元,第二个村民卖出的单价为$\frac {20}{x}$元,根据题意,得$x\cdot \frac {45}{100-x}=(100-x)\cdot \frac {20}{x}$.解得x=40或x=-200(舍去).$\therefore 100-40=60$(个),$40×\frac {45}{100-40}=30$(元).答:第一个村民有40个鸡蛋,第二个村民有60个鸡蛋,都卖了30元.