《2025年三维数字课堂九年级数学上册人教版》

1. 自由落体公式：$h= \frac{1}{2}gt^{2}$(其中$g$为常量),$h与t$之间的关系是(C)
A.正比例函数
B.一次函数
C.二次函数
D.以上答案都不对

答案： C

2. 下列函数中,是二次函数的有(B)
①$y= x+\frac{1}{2}$；②$y= 3(x+1)^{2}-1$；③$y= (x+3)^{2}-2x^{2}$；④$y= \frac{1}{x^{2}}+x$。
A.1 个
B.2 个
C.3 个
D.4 个

答案： B

3. 下列函数是$y关于x$的二次函数的是(C)
A.$y= \frac{3}{x}$
B.$y= x+2$
C.$y= -3x^{2}$
D.$y= \sqrt{x-3}$

答案： C 点拨:只有y=-3x²是形如y=ax²+bx+c(a≠0)的函数,是二次函数.故选C.

4. 二次函数$y= 2x^{2}-3$的二次项系数、一次项系数和常数项分别是(A)
A.2、0、-3
B.2、-3、0
C.2、3、0
D.2、0、3

答案： A 点拨:二次函数y=2x²-3的二次项系数是2,一次项系数是0,常数项是-3.故选A.

5. 二次函数$y= -2x^{2}+x-2$的二次项系数为-2,一次项系数为1,常数项为-2。

答案： -2 1 -2

6. 已知梯形的面积为$y\ cm^{2}$,下底与高都是$x\ cm$,上底长是下底长的$\frac{1}{3}$,那么$y与x$的函数关系式为y=2/3x²。

答案： y=2/3x²

7. 下列函数：①$y= -2x^{2}$；②$y= 2x$；③$y= 2^{2}+x^{2}-x^{3}$；④$y= 3-t-t^{2}$。其中是二次函数的是①④。($x$、$t$为自变量,填序号)

答案： ①④

8. 当$k$为何值时,函数$y= (k-1)x^{k^{2}+k}+1$为二次函数？

答案： $k = -2$。

9. 如图 22-1-1,矩形的长是 4 cm,宽是 3 cm,如果将长和宽都增加$x\ cm$,那么面积增加$y\ cm^{2}$。
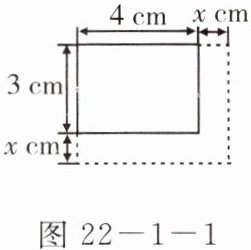
(1) 求$y与x$之间的函数关系式；
(2) 当边长增加多少时,面积增加$8\ cm^{2}$？

答案：
(1)原来的面积是3×4=12(cm²),现在的面积是(4+x)(3+x)cm²,
∴y=(4+x)(3+x)-12=x²+7x.
(2)由题意,得8=x²+7x,
∴x₁=1,x₂=-8(舍去).即当边长增加1cm时,面积增加8cm².点拨:表示简单变量之间的函数关系,要找到问题的切入点,即存在怎样的等量关系.