第31页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
3. 在平面直角坐标系中,若将抛物线 $ y = 2x^{2} - 4x + 3 $ 先向右平移 $ 3 $ 个单位,再向上平移 $ 2 $ 个单位,则经过这两次平移后所得抛物线的顶点坐标是(
A.$ (-2,3) $
B.$ (-1,4) $
C.$ (1,4) $
D.$ (4,3) $
D
)A.$ (-2,3) $
B.$ (-1,4) $
C.$ (1,4) $
D.$ (4,3) $
答案:
D
4. 一跳水运动员从 $ 10 $ 米高跳台上跳下,他的高度 $ h $(米)与所用时间 $ t $(秒)的关系为 $ h = -5(t - 2)(t + 1) $,则他跳起
0.5
秒达到最大高度,最大高度是 11.25
米。
答案:
0.5 11.25
5. 如图 $ 22 - 6 - 2 $,已知二次函数 $ y = -\frac{1}{2}x^{2} + bx + c $ 的图象经过 $ A(2,0) $,$ B(0,-6) $ 两点。
(1) 求这个二次函数的表达式;
(2) 设该二次函数的对称轴与 $ x $ 轴交于点 $ C $,连接 $ BA $、$ BC $,求 $ \triangle ABC $ 的面积。
]
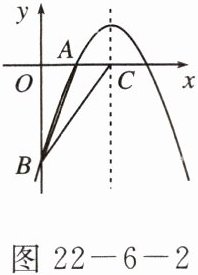
(1) 求这个二次函数的表达式;
(2) 设该二次函数的对称轴与 $ x $ 轴交于点 $ C $,连接 $ BA $、$ BC $,求 $ \triangle ABC $ 的面积。
]

答案:
解:
(1)把$A(2,0),B(0,-6)$代入$y=-\frac{1}{2}x^{2}+bx+c$得$\begin{cases}-2 + 2b + c = 0\\c = -6\end{cases}$,解得$\begin{cases}b = 4\\c = -6\end{cases}$
∴$y=-\frac{1}{2}x^{2}+4x-6.$
(2)
∵该抛物线的对称轴为直线$x=-\frac{4}{2×(-\frac{1}{2})}=4$
∴点C的坐标为$(4,0).$
∴$AC = OC - OA = 4 - 2 = 2.$
∴$S_{\triangle ABC}=\frac{1}{2}×AC×OB=\frac{1}{2}×2×6=6.$
(1)把$A(2,0),B(0,-6)$代入$y=-\frac{1}{2}x^{2}+bx+c$得$\begin{cases}-2 + 2b + c = 0\\c = -6\end{cases}$,解得$\begin{cases}b = 4\\c = -6\end{cases}$
∴$y=-\frac{1}{2}x^{2}+4x-6.$
(2)
∵该抛物线的对称轴为直线$x=-\frac{4}{2×(-\frac{1}{2})}=4$
∴点C的坐标为$(4,0).$
∴$AC = OC - OA = 4 - 2 = 2.$
∴$S_{\triangle ABC}=\frac{1}{2}×AC×OB=\frac{1}{2}×2×6=6.$
已知在 $ Rt\triangle OAB $ 中,$ \angle OAB = 90^{\circ} $,$ \angle BOA = 30^{\circ} $,$ AB = 2 $,若以 $ O $ 为坐标原点,$ OA $ 所在直线为 $ x $ 轴,建立如图 $ 22 - 6 - 3 $ 所示的平面直角坐标系,点 $ B $ 在第一象限内,将 $ Rt\triangle OAB $ 沿 $ OB $ 折叠后,点 $ A $ 落在第一象限内的点 $ C $ 处。
(1) 求点 $ C $ 的坐标;
(2) 若抛物线 $ y = ax^{2} + bx(a \neq 0) $ 经过 $ C $、$ A $ 两点,求此抛物线的解析式;
(3) 若抛物线的对称轴与 $ OB $ 交于点 $ D $,点 $ P $ 为线段 $ DB $ 上一点,过点 $ P $ 作 $ y $ 轴的平行线,交抛物线于点 $ M $。问是否存在这样的点 $ P $,使四边形 $ CDPM $ 为等腰梯形?若存在,请求出此时点 $ P $ 的坐标;若不存在,请说明理由。
]
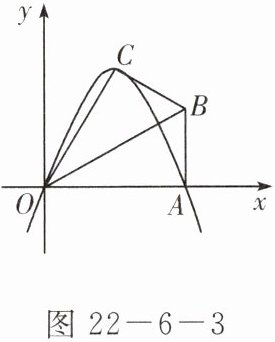
(1) 求点 $ C $ 的坐标;
(2) 若抛物线 $ y = ax^{2} + bx(a \neq 0) $ 经过 $ C $、$ A $ 两点,求此抛物线的解析式;
(3) 若抛物线的对称轴与 $ OB $ 交于点 $ D $,点 $ P $ 为线段 $ DB $ 上一点,过点 $ P $ 作 $ y $ 轴的平行线,交抛物线于点 $ M $。问是否存在这样的点 $ P $,使四边形 $ CDPM $ 为等腰梯形?若存在,请求出此时点 $ P $ 的坐标;若不存在,请说明理由。
]

答案:
解:
(1)如答图,过点C作$CH⊥x$轴,垂足为H.
∵在$Rt\triangle OAB$中,$∠OAB = 90^{\circ},∠BOA = 30^{\circ},AB = 2$
∴$OB = 4,OA = 2\sqrt{3}$由折叠知,$∠COB = 30^{\circ},OC = OA = 2\sqrt{3}$
∴$∠COH = 60^{\circ},OH = \sqrt{3},CH = 3.$
∴C点的坐标为$(\sqrt{3},3).(2)∵抛物线$y = ax^{2}+bx(a≠0)$经过$C(\sqrt{3},3)$、$A(2\sqrt{3},0)$两点∴$\begin{cases}3 = (\sqrt{3})^{2}a + \sqrt{3}b\\0 = (2\sqrt{3})^{2}a + 2\sqrt{3}b\end{cases}$,解得$\begin{cases}a = -1\\b = 2\sqrt{3}\end{cases}$∴此抛物线的解析式为$y = -x^{2}+2\sqrt{3}x.
(3)存在.$y = -x^{2}+2\sqrt{3}x$的顶点坐标为$(\sqrt{3},3)$,即为点C.如答图,$MP⊥x$轴,设垂足为N,$PN = t.$
∵$∠BOA = 30^{\circ}$
∴$ON = \sqrt{3}t.$
∴$P(\sqrt{3}t,t).$作$PQ⊥CD$,垂足为Q,$ME⊥CD$,垂足为E;把$x = \sqrt{3}t$代入$y = -x^{2}+2\sqrt{3}x$得$y = -3t^{2}+6t.$
∴$M(\sqrt{3}t,-3t^{2}+6t),E(\sqrt{3},-3t^{2}+6t).$同理:$Q(\sqrt{3},t),D(\sqrt{3},1).$要使四边形CDPM为等腰梯形,只需$CE = QD$,即$3 - (-3t^{2}+6t)=t - 1$,解得$t_1 = \frac{4}{3},t_2 = 1$(舍去).
∴P点坐标为$(\frac{4}{3}\sqrt{3},\frac{4}{3}).$
∴存在满足条件的点P,使得四边形CDPM为等腰梯形,此时P点的坐标为$(\frac{4}{3}\sqrt{3},\frac{4}{3}).$
(1)如答图,过点C作$CH⊥x$轴,垂足为H.
∵在$Rt\triangle OAB$中,$∠OAB = 90^{\circ},∠BOA = 30^{\circ},AB = 2$
∴$OB = 4,OA = 2\sqrt{3}$由折叠知,$∠COB = 30^{\circ},OC = OA = 2\sqrt{3}$
∴$∠COH = 60^{\circ},OH = \sqrt{3},CH = 3.$
∴C点的坐标为$(\sqrt{3},3).(2)∵抛物线$y = ax^{2}+bx(a≠0)$经过$C(\sqrt{3},3)$、$A(2\sqrt{3},0)$两点∴$\begin{cases}3 = (\sqrt{3})^{2}a + \sqrt{3}b\\0 = (2\sqrt{3})^{2}a + 2\sqrt{3}b\end{cases}$,解得$\begin{cases}a = -1\\b = 2\sqrt{3}\end{cases}$∴此抛物线的解析式为$y = -x^{2}+2\sqrt{3}x.
(3)存在.$y = -x^{2}+2\sqrt{3}x$的顶点坐标为$(\sqrt{3},3)$,即为点C.如答图,$MP⊥x$轴,设垂足为N,$PN = t.$
∵$∠BOA = 30^{\circ}$
∴$ON = \sqrt{3}t.$
∴$P(\sqrt{3}t,t).$作$PQ⊥CD$,垂足为Q,$ME⊥CD$,垂足为E;把$x = \sqrt{3}t$代入$y = -x^{2}+2\sqrt{3}x$得$y = -3t^{2}+6t.$
∴$M(\sqrt{3}t,-3t^{2}+6t),E(\sqrt{3},-3t^{2}+6t).$同理:$Q(\sqrt{3},t),D(\sqrt{3},1).$要使四边形CDPM为等腰梯形,只需$CE = QD$,即$3 - (-3t^{2}+6t)=t - 1$,解得$t_1 = \frac{4}{3},t_2 = 1$(舍去).
∴P点坐标为$(\frac{4}{3}\sqrt{3},\frac{4}{3}).$
∴存在满足条件的点P,使得四边形CDPM为等腰梯形,此时P点的坐标为$(\frac{4}{3}\sqrt{3},\frac{4}{3}).$
查看更多完整答案,请扫码查看


