第76页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
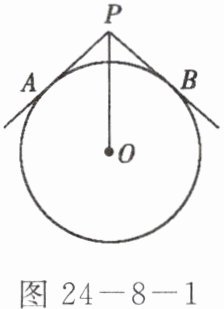
1. 如图 24-8-1 所示,$\odot O$的半径为 2,直线$PA$,$PB为\odot O$的切线,$A$,$B$为切点,若$PA\perp PB$,则$OP$的长为(
A.$4\sqrt{2}$
B.4
C.$2\sqrt{2}$
D.2
]
C
)
A.$4\sqrt{2}$
B.4
C.$2\sqrt{2}$
D.2
]
答案:
C 点拨:连接OA,OB,所以可得四边形OBPA是正方形,所以OA=PA=2,由勾股定理可知OP的长为$2\sqrt{2}$.
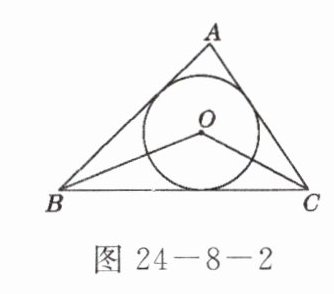
2. 如图 24-8-2,点$O是\triangle ABC$的内切圆的圆心,若$\angle BAC = 80^{\circ}$,则$\angle BOC$等于(
A.$130^{\circ}$
B.$100^{\circ}$
C.$50^{\circ}$
D.$65^{\circ}$
A
)
A.$130^{\circ}$
B.$100^{\circ}$
C.$50^{\circ}$
D.$65^{\circ}$
答案:
A 点拨:三角形内切圆的圆心是三角形三条角平分线的交点.
3. 下列说法正确的有(
①任意一个三角形都有且只有一个内切圆;
②三角形的内心都在三角形的内部;
③三角形的内心到三角形各顶点的距离相等;
④三角形的内心与三角形各顶点的连线分别平分这个三角形的三个内角.
A.1 个
B.2 个
C.3 个
D.4 个
C
)①任意一个三角形都有且只有一个内切圆;
②三角形的内心都在三角形的内部;
③三角形的内心到三角形各顶点的距离相等;
④三角形的内心与三角形各顶点的连线分别平分这个三角形的三个内角.
A.1 个
B.2 个
C.3 个
D.4 个
答案:
C
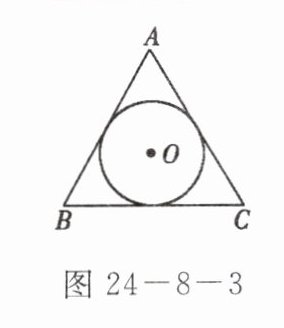
4. 如图 24-8-3 所示,$\odot O$是边长为 2 的等边三角形$ABC$的内切圆,则$\odot O$的半径为
]
$\frac{\sqrt{3}}{3}$
.]

答案:
$\frac{\sqrt{3}}{3}$
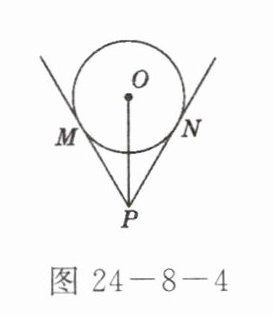
5. 一根钢管放在 V 形架内,如图 24-8-4 是其截面图,$O$为钢管的圆心. 如果钢管的半径为 25 cm,$\angle MPN = 60^{\circ}$,则$OP = $
50cm
.
答案:
50cm 点拨:连接ON,则ON⊥PN.利用切线长定理,得出∠OPN=30°,再利用直角三角形中30°角所对的直角边与斜边的关系得出OP的长.
6. 如图 24-8-5,$PA$,$PB是\odot O$的切线,$A$,$B$为切点,$\angle OAB = 38^{\circ}$,则$\angle P = $

76
$^{\circ}$.
答案:
76 点拨:
∵PA,PB是$\odot O$的切线,
∴PA=PB,PA⊥OA,
∴∠PAB=∠PBA,∠OAP=90°,
∴∠PBA=∠PAB=90°−∠OAB=90°−38°=52°,
∴∠P=180°−52°−52°=76°.
∵PA,PB是$\odot O$的切线,
∴PA=PB,PA⊥OA,
∴∠PAB=∠PBA,∠OAP=90°,
∴∠PBA=∠PAB=90°−∠OAB=90°−38°=52°,
∴∠P=180°−52°−52°=76°.
7. 如图 24-8-6,$PA$,$PB是\odot O$的两条切线,$A$,$B$为切点,如果$OP = 4$,$PA = 2\sqrt{3}$,求$\angle AOB$的度数.
]
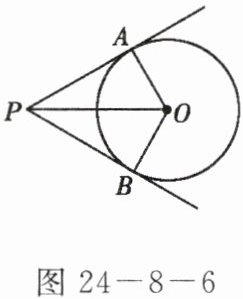
]

答案:
解:
∵PA,PB是$\odot O$的切线,切点为A,B,
∴OA⊥PA,OB⊥PB,∠APO=∠BPO,
∴∠AOP=∠BOP.在Rt△PAO中,由勾股定理,得$OA^{2}=OP^{2}-PA^{2}=4^{2}-(2\sqrt{3})^{2}=4$,
∴OA=2,又
∵OP=4,
∴OA=$\frac{1}{2}$OP,
∴∠APO=30°,
∴∠AOP=60°,
∴∠AOB=2∠AOP=120°.
∵PA,PB是$\odot O$的切线,切点为A,B,
∴OA⊥PA,OB⊥PB,∠APO=∠BPO,
∴∠AOP=∠BOP.在Rt△PAO中,由勾股定理,得$OA^{2}=OP^{2}-PA^{2}=4^{2}-(2\sqrt{3})^{2}=4$,
∴OA=2,又
∵OP=4,
∴OA=$\frac{1}{2}$OP,
∴∠APO=30°,
∴∠AOP=60°,
∴∠AOB=2∠AOP=120°.
8. 如图 24-8-7,$AB为\odot O$的直径,$C为\odot O$上一点,$D为\overset{\frown}{BC}$的中点,过点$D作直线AC$的垂线,垂足为$E$,连接$OD$.
(1)求证:$\angle A = \angle DOB$;
(2)$DE与\odot O$有怎样的位置关系?请说明理由.
]
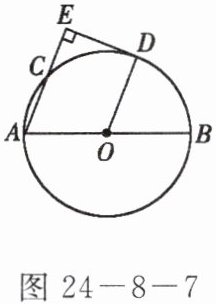
(1)求证:$\angle A = \angle DOB$;
(2)$DE与\odot O$有怎样的位置关系?请说明理由.
]

答案:
(1)证明:如答图24−8−1.连接OC,
∵D为$\widehat{BC}$的中点,
∴$\widehat{CD}=\widehat{BD}$,
∴∠BOD=$\frac{1}{2}$∠BOC.
∵∠BAC=$\frac{1}{2}$∠BOC,
∴∠A=∠DOB.

答图24−8−1
(2)解:DE与$\odot O$相切.理由:
∵∠A=∠DOB,
∴AE//OD.
∵DE⊥AE,
∴OD⊥DE,
∴DE与$\odot O$相切.
(1)证明:如答图24−8−1.连接OC,
∵D为$\widehat{BC}$的中点,
∴$\widehat{CD}=\widehat{BD}$,
∴∠BOD=$\frac{1}{2}$∠BOC.
∵∠BAC=$\frac{1}{2}$∠BOC,
∴∠A=∠DOB.

答图24−8−1
(2)解:DE与$\odot O$相切.理由:
∵∠A=∠DOB,
∴AE//OD.
∵DE⊥AE,
∴OD⊥DE,
∴DE与$\odot O$相切.
查看更多完整答案,请扫码查看


