《2025年三维数字课堂九年级数学上册人教版》

8. 生产某种产品,原来的成本价为500元,销售价为625元,经市场预测,该产品的销售价第一个月将降低20%,第二个月将比第一个月提高6%,为了使两个月后的销售利润不变,该产品的成本价平均每月应降低百分之几？

答案： 解:设成本价平均每月降低的百分数为x,则$625×(1-20\% )×(1+6\% )-500(1-x)^{2}=625-500$,解得$x_{1}=0.1=10\% ,x_{2}=1.9$(舍去).答:该产品的成本价平均每月应降低10%.

1. 某市2023年生产总值比2022年增长了12%,由于受洪涝灾害的影响,2024年比2023年增长7%,若这两年生产总值年平均增长率为$x\%$,则$x\%$满足的方程是(D)
A.$12\%+7\%= x\%$
B.$(1+12\%)(1+7\%)= 2(1+x\%)$
C.$12\%+7\%= 2x\%$
D.$(1+12\%)(1+7\%)= (1+x\%)^{2}$

答案： D

2. 某网店销售运动鞋,若每双盈利40元,每天可以销售20双,该网店决定适当降价促销,经调查得知,每双运动鞋每降价1元,每天可多销售2双,若想每天盈利1200元,并尽可能让利于顾客,赢得市场,则每双运动鞋应降价(B)
A.10元或20元
B.20元
C.5元
D.5元或10元

答案： B

3. 把一个小球以20m/s的速度竖直向上抛出,它在空中的高度$h$(m)与时间$t$(s)满足关系$h= 20t-5t^{2}$,当$h= 20$时,小球的运动时间为2s.

答案： 2

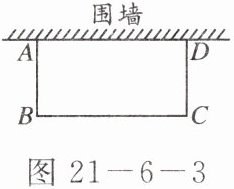
4. 如图21-6-3,邻边不相等的矩形花圃$ABCD$,它的一边$AD$利用已有的围墙,另外三边所围的栅栏的总长度是6m.若矩形的面积为$4m^{2}$,则$AB$的长度是1m.(可利用的围墙长度超过6m)

答案： 1

5. 一个两位数的十位上的数字比个位上的数字小4,十位上的数字的平方与个位上的数字的平方之和等于这个数的十位和个位上的数字之和的5倍,则这个两位数是26.

答案： 26

6. 在一次象棋比赛中,实行单循环赛制(即每个选手都与其他选手比赛一局),每局胜者记2分,负者记0分,如果平局,两名选手各记1分,今有4名同学统计了比赛中全部选手的得分总和,结果分别为2005分、2004分、2070分、2008分,经核实确定只有一名同学统计无误,试计算这次比赛中共有多少名选手参赛.

答案： 解:设共有x(x为正整数)名选手参赛,所以共有$\frac {1}{2}x(x-1)$局比赛.因为每局比赛共记2分,所以全部选手的得分总和为x(x-1)分,由于相邻两个自然数之积是偶数,且其个位数字只能是0,2,6,故总得分不能为2005分,2004分,2008分,所以可得方程$x(x-1)=2070$.解得$x_{1}=46,x_{2}=-45$(不符合题意,舍去).答:这次比赛共有46名选手参赛.