第77页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
解方程。
$3x - \frac{1}{3} = \frac{1}{6}$
$\frac{5}{18}x + \frac{3}{4}x = \frac{3}{2}$
$(1 - \frac{2}{7})x = 25$
$3x - \frac{1}{3} = \frac{1}{6}$
$\frac{5}{18}x + \frac{3}{4}x = \frac{3}{2}$
$(1 - \frac{2}{7})x = 25$
答案:
解析:
这些题目都是基础的一元一次方程,需要通过移项、合并同类项、化简等步骤求解。
答案:
(1)
解:$3x - \frac{1}{3} = \frac{1}{6}$,
移项得:$3x = \frac{1}{6} + \frac{1}{3}$,
即:$3x = \frac{1+2}{6} = \frac{1}{2}$,
系数化为$1$得:$x = \frac{1}{2} ÷ 3 = \frac{1}{6}$;
(2)
解:$\frac{5}{18}x + \frac{3}{4}x = \frac{3}{2}$,
合并同类项得:$(\frac{5}{18} + \frac{3}{4})x = \frac{3}{2}$,
即:$(\frac{10+27}{36})x = \frac{3}{2}$,
化简得:$\frac{37}{36}x = \frac{3}{2}$,
系数化为$1$得:$x = \frac{3}{2} × \frac{36}{37} = \frac{54}{37}$;
(3)
解:$(1 - \frac{2}{7})x = 25$,
化简得:$\frac{5}{7}x = 25$,
系数化为$1$得:$x = 25 ÷ \frac{5}{7} = 25 × \frac{7}{5} = 35$。
这些题目都是基础的一元一次方程,需要通过移项、合并同类项、化简等步骤求解。
答案:
(1)
解:$3x - \frac{1}{3} = \frac{1}{6}$,
移项得:$3x = \frac{1}{6} + \frac{1}{3}$,
即:$3x = \frac{1+2}{6} = \frac{1}{2}$,
系数化为$1$得:$x = \frac{1}{2} ÷ 3 = \frac{1}{6}$;
(2)
解:$\frac{5}{18}x + \frac{3}{4}x = \frac{3}{2}$,
合并同类项得:$(\frac{5}{18} + \frac{3}{4})x = \frac{3}{2}$,
即:$(\frac{10+27}{36})x = \frac{3}{2}$,
化简得:$\frac{37}{36}x = \frac{3}{2}$,
系数化为$1$得:$x = \frac{3}{2} × \frac{36}{37} = \frac{54}{37}$;
(3)
解:$(1 - \frac{2}{7})x = 25$,
化简得:$\frac{5}{7}x = 25$,
系数化为$1$得:$x = 25 ÷ \frac{5}{7} = 25 × \frac{7}{5} = 35$。
看图列式计算。
①
甲厂:?台
乙厂:比甲厂少$\frac{1}{5}$,2000台
②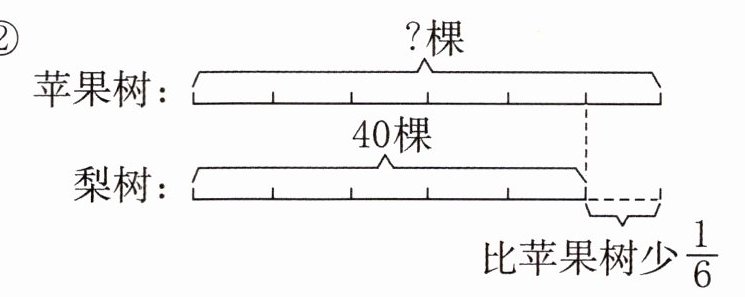
苹果树:?棵
梨树:40棵,比苹果树少$\frac{1}{6}$
①

甲厂:?台
乙厂:比甲厂少$\frac{1}{5}$,2000台
②

苹果树:?棵
梨树:40棵,比苹果树少$\frac{1}{6}$
答案:
①解析:本题考查利用分数除法解决“已知比一个数少几分之几的数是多少,求这个数”的实际问题。
乙厂比甲厂少$\frac{1}{5}$,是把甲厂的台数看作单位“$1$”,那么乙厂的台数是甲厂的$1 - \frac{1}{5}=\frac{4}{5}$。已知乙厂有$2000$台,求甲厂的台数,用除法计算。
答案:
$2000÷(1 - \frac{1}{5})$
$=2000÷\frac{4}{5}$
$=2000×\frac{5}{4}$
$ = 2500$(台)
答:甲厂有$2500$台。
②解析:本题考查利用分数除法解决“已知比一个数少几分之几的数是多少,求这个数”的实际问题。
梨树比苹果树少$\frac{1}{6}$,是把苹果树的棵数看作单位“$1$”,那么梨树的棵数是苹果树的$1 - \frac{1}{6}=\frac{5}{6}$。已知梨树有$40$棵,求苹果树的棵数,用除法计算。
答案:
$40÷(1 - \frac{1}{6})$
$=40÷\frac{5}{6}$
$=40×\frac{6}{5}$
$ = 48$(棵)
答:苹果树有$48$棵。
乙厂比甲厂少$\frac{1}{5}$,是把甲厂的台数看作单位“$1$”,那么乙厂的台数是甲厂的$1 - \frac{1}{5}=\frac{4}{5}$。已知乙厂有$2000$台,求甲厂的台数,用除法计算。
答案:
$2000÷(1 - \frac{1}{5})$
$=2000÷\frac{4}{5}$
$=2000×\frac{5}{4}$
$ = 2500$(台)
答:甲厂有$2500$台。
②解析:本题考查利用分数除法解决“已知比一个数少几分之几的数是多少,求这个数”的实际问题。
梨树比苹果树少$\frac{1}{6}$,是把苹果树的棵数看作单位“$1$”,那么梨树的棵数是苹果树的$1 - \frac{1}{6}=\frac{5}{6}$。已知梨树有$40$棵,求苹果树的棵数,用除法计算。
答案:
$40÷(1 - \frac{1}{6})$
$=40÷\frac{5}{6}$
$=40×\frac{6}{5}$
$ = 48$(棵)
答:苹果树有$48$棵。
列方程解决问题。
① 某渔船上午捕鱼1200千克,比下午少捕$\frac{1}{6}$。该渔船下午捕鱼多少千克?
② 一只鲨鱼每小时可以游50千米,比一只海豚慢$\frac{1}{11}$。这只海豚每小时可以游多少千米?
③ 一件上衣和一条裤子共420元,其中裤子的价格是上衣的$\frac{3}{4}$。裤子和上衣的价格分别是多少元?
① 某渔船上午捕鱼1200千克,比下午少捕$\frac{1}{6}$。该渔船下午捕鱼多少千克?
② 一只鲨鱼每小时可以游50千米,比一只海豚慢$\frac{1}{11}$。这只海豚每小时可以游多少千米?
③ 一件上衣和一条裤子共420元,其中裤子的价格是上衣的$\frac{3}{4}$。裤子和上衣的价格分别是多少元?
答案:
①解:设该渔船下午捕鱼$x$千克。
$x-\frac{1}{6}x=1200$
$\frac{5}{6}x=1200$
$x=1200÷\frac{5}{6}$
$x=1440$
答:该渔船下午捕鱼1440千克。
②解:设这只海豚每小时可以游$x$千米。
$x-\frac{1}{11}x=50$
$\frac{10}{11}x=50$
$x=50÷\frac{10}{11}$
$x=55$
答:这只海豚每小时可以游55千米。
③解:设上衣的价格是$x$元,则裤子的价格是$\frac{3}{4}x$元。
$x+\frac{3}{4}x=420$
$\frac{7}{4}x=420$
$x=420÷\frac{7}{4}$
$x=240$
$\frac{3}{4}x=\frac{3}{4}×240 = 180$
答:上衣的价格是240元,裤子的价格是180元。
$x-\frac{1}{6}x=1200$
$\frac{5}{6}x=1200$
$x=1200÷\frac{5}{6}$
$x=1440$
答:该渔船下午捕鱼1440千克。
②解:设这只海豚每小时可以游$x$千米。
$x-\frac{1}{11}x=50$
$\frac{10}{11}x=50$
$x=50÷\frac{10}{11}$
$x=55$
答:这只海豚每小时可以游55千米。
③解:设上衣的价格是$x$元,则裤子的价格是$\frac{3}{4}x$元。
$x+\frac{3}{4}x=420$
$\frac{7}{4}x=420$
$x=420÷\frac{7}{4}$
$x=240$
$\frac{3}{4}x=\frac{3}{4}×240 = 180$
答:上衣的价格是240元,裤子的价格是180元。
查看更多完整答案,请扫码查看


