《2025年口算题卡升级练五年级上册青岛版54制》

1. 计算下列题,能简算的要简算。
$15 - \frac{8}{9} × \frac{3}{8} × 6$
$(\frac{1}{12} - \frac{1}{16}) × \frac{48}{49}$
$\frac{1}{12} + \frac{1}{4} × \frac{4}{5} - \frac{1}{8}$
$\frac{7}{12} × (\frac{3}{14} + \frac{4}{7})$


$(\frac{1}{6} + \frac{3}{4} - \frac{2}{3}) × 12$
$\frac{4}{9} ÷ [\frac{4}{5} - (\frac{1}{5} + \frac{1}{3})]$

答案： 1. 
$\;\;\;\;15 - \frac{8}{9} × \frac{3}{8} × 6$
$=15 - \frac{1}{3} × 6$
$=15 - 2$
$= 13$
2. 
$\;\;\;\;(\frac{1}{12} - \frac{1}{16}) × \frac{48}{49}$
$=(\frac{4}{48} - \frac{3}{48}) × \frac{48}{49}$
$=\frac{1}{48} × \frac{48}{49}$
$= \frac{1}{49}$
3. 
$\;\;\;\;\frac{1}{12} + \frac{1}{4} × \frac{4}{5} - \frac{1}{8}$
$=\frac{1}{12} + \frac{1}{5} - \frac{1}{8}$
$=\frac{10}{120} + \frac{24}{120} - \frac{15}{120}$
$=\frac{19}{120}$
4. 
$\;\;\;\;\frac{7}{12} × (\frac{3}{14} + \frac{4}{7})$
$=\frac{7}{12} × (\frac{3}{14} + \frac{8}{14})$
$=\frac{7}{12} × \frac{11}{14}$
$= \frac{11}{24}$
5. 
$\;\;\;\;(\frac{1}{6} + \frac{3}{4} - \frac{2}{3}) × 12$
$=(\frac{2}{12} + \frac{9}{12} - \frac{8}{12}) × 12$
$=\frac{3}{12} × 12$
$= 3$
6. 
$\;\;\;\;\frac{4}{9} ÷ [\frac{4}{5} - (\frac{1}{5} + \frac{1}{3})]$
$=\frac{4}{9} ÷ [\frac{4}{5} - \frac{1}{5} - \frac{1}{3}]$
$=\frac{4}{9} ÷ [\frac{3}{5} - \frac{1}{3}]$
$=\frac{4}{9} ÷ [\frac{9}{15} - \frac{5}{15}]$
$=\frac{4}{9} ÷ \frac{4}{15}$
$=\frac{4}{9} × \frac{15}{4}$
$=\frac{5}{3}$

2. 解方程。
$x - \frac{1}{4}x = \frac{9}{16}$
$x + \frac{1}{6}x = 21$
$\frac{1}{2}x + x = 15$
$(3 - \frac{1}{3})x = 24$
$5x ÷ \frac{2}{3} = \frac{3}{5}$
$x - \frac{2}{3}x = 30$

答案： 解析：
这些题目都是解一元一次方程的问题，需要我们将方程进行化简，通过合并同类项、移项等方法，求出$x$的值。
答案：
(1)解：$x - \frac{1}{4}x = \frac{9}{16}$
合并同类项得：$\frac{3}{4}x = \frac{9}{16}$，
系数化为$1$得：$x = \frac{9}{16} × \frac{4}{3} = \frac{3}{4}$；
(2)解：$x + \frac{1}{6}x = 21$
合并同类项得：$\frac{7}{6}x = 21$，
系数化为$1$得：$x = 21 × \frac{6}{7} = 18$；
(3)解：$\frac{1}{2}x + x = 15$
合并同类项得：$\frac{3}{2}x = 15$，
系数化为$1$得：$x = 15 × \frac{2}{3} = 10$；
(4)解：$(3 - \frac{1}{3})x = 24$
化简得：$\frac{8}{3}x = 24$，
系数化为$1$得：$x = 24 × \frac{3}{8} = 9$；
(5)解：$5x ÷ \frac{2}{3} = \frac{3}{5}$
化简得：$5x= \frac{3}{5} × \frac{2}{3} =\frac{2}{5}$，
系数化为$1$得：$x =\frac{2}{5} × \frac{1}{5} = \frac{2}{25}$；
(6)解：$x - \frac{2}{3}x = 30$
合并同类项得：$\frac{1}{3}x = 30$，
系数化为$1$得：$x = 30 × 3 = 90$。

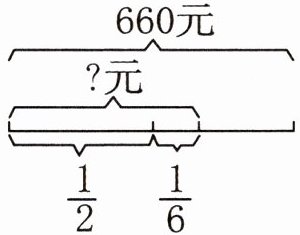
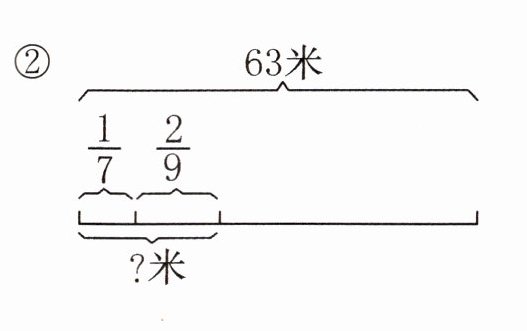
3. 看图列式计算。

答案： 1. 对于①：
解：
先求总共占的比例：$\frac{1}{2}+\frac{1}{6}=\frac{3 + 1}{6}=\frac{4}{6}=\frac{2}{3}$。
已知总数是$660$元，根据“求一个数的几分之几是多少用乘法”，则$660×(\frac{1}{2}+\frac{1}{6})$。
计算$660×\frac{2}{3}=440$（元）。
2. 对于②：
解：
先求总共占的比例：$\frac{1}{7}+\frac{2}{9}=\frac{9+14}{63}=\frac{23}{63}$。
已知总数是$63$米，根据“求一个数的几分之几是多少用乘法”，则$63×(\frac{1}{7}+\frac{2}{9})$。
计算$63×\frac{23}{63}=23$（米）。
综上，①的结果是$440$元；②的结果是$23$米。