《2025年全效学习课时提优九年级数学全一册人教版精华版》

在如图所示的图形中随机撒一把豆子,计算落在A,B,C三个区域中的豆子数的比.多次重复这个试验,你能否发现上述比与A,B,C三个区域的面积有什么关系?把“在图形中随机撒豆子”作为试验,把“豆子落在区域C中”记作事件W,估计事件W的概率P(W)的值.

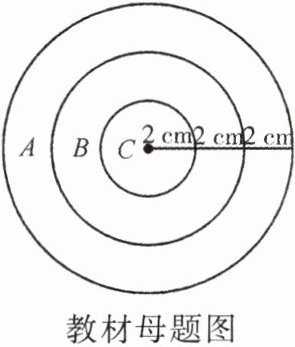
答案： 落在A,B,C三个区域中的豆子数的比等于A,B,C三个区域的面积比.$P(W)=\frac {1}{9}$

1. 如图,在两个同心圆中,三条直径把大圆分成六等份.若在这个圆面上均匀地撒一把豆子,则豆子落在阴影部分的概率是______.

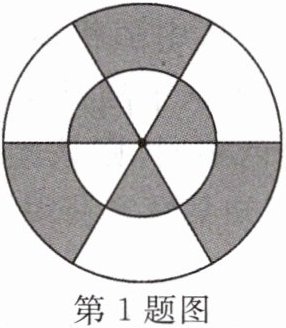
答案： $\frac {1}{2}$

2. 如图,顺次连接正方形ABCD各边的中点得到四边形EFGH,顺次连接四边形EFGH各边的中点得到四边形JKLM.若向正方形ABCD中随机撒一粒豆子,则它落在阴影部分的概率是______.

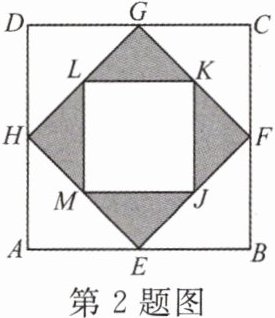
答案： $\frac {1}{4}$

3. 如图,在正方形ABCD中,分别以点B,D为圆心,正方形的边长2为半径画弧,形成阴影部分的“树叶”图案.
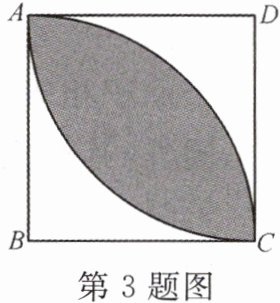
(1)求以点B为圆心的$\overset{\frown}{AC}$的长和阴影部分的面积($\pi$取3)；
(2)若在正方形ABCD中随机撒一粒豆子,求豆子落在阴影区域内的概率(豆子落在弧上不计).

答案：
(1)2
(2)$\frac {1}{2}$

4. 如图,在一不规则区域内,有一边长为$3\sqrt{3}\ m$的正方形,向区域内随机地撒4000粒黄豆,数得落在正方形区域内(含边界)的黄豆有1350粒,以此实验数据为依据,回答下面问题：
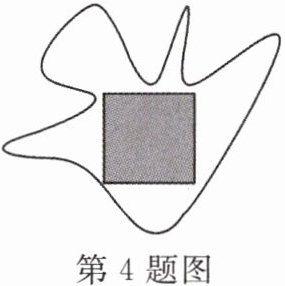
(1)随机向不规则区域内掷一粒黄豆,求黄豆落在正方形区域内(含边界)的概率；
(2)请你估计出该不规则图形的面积.

答案：
(1)$\frac {27}{80}$
(2)$80m^{2}$