《2025年全效学习课时提优九年级数学全一册人教版精华版》

1. 二次函数 $ y= x^{2}+bx+c $ 的图象经过四个点 $(-1,0),(0,y_{1}),(1,y_{2}),(2,y_{3})$. 若 $ y_{2}＜y_{1}＜y_{3} $,则 $ y_{2} $ 的取值范围是 ( )

A.$-4＜y_{2}＜-2$
B.$-2＜y_{2}＜0$
C.$0＜y_{2}＜2$
D.$2＜y_{2}＜4$

答案： A

2. 如图,二次函数 $ y= ax^{2}+bx+c $ 的部分图象与 $ x $ 轴的一个交点的横坐标是-3,顶点坐标为 $(-1,4)$,则下列说法正确的是 ( )


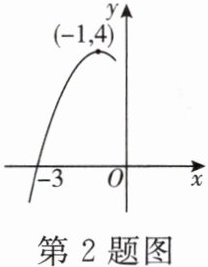
A.二次函数图象的对称轴是直线 $ x= 1 $
B.二次函数图象与 $ x $ 轴的另一个交点的横坐标是 2
C.当 $ x＜-1 $ 时,$ y $ 随 $ x $ 的增大而减小
D.二次函数图象与 $ y $ 轴的交点的纵坐标是 3

答案： D

3. 已知二次函数 $ y= ax^{2}+(2a-3)x+a-1 $($ x $ 是自变量)的图象经过第一、二、四象限,则实数 $ a $ 的取值范围是 ( )

A.$1\leqslant a＜\frac{9}{8}$
B.$0＜a＜\frac{9}{5}$
C.$0＜a＜\frac{9}{8}$
D.$1\leqslant a＜\frac{3}{2}$

答案： A

4. 将抛物线 $ y= x^{2}-6x+5 $ 先向右平移 1 个单位长度,再向上平移 2 个单位长度,得到的抛物线的解析式为 ( )

A.$ y= (x-4)^{2}-6 $
B.$ y= (x-1)^{2}-3 $
C.$ y= (x-2)^{2}-2 $
D.$ y= (x-4)^{2}-2 $

答案： D

5. 将抛物线 $ y= (x+3)^{2} $ 向下平移 1 个单位长度,再向右平移 ______ 个单位长度后,得到的新抛物线经过原点.

答案： 2或4

6. 已知二次函数 $ y= ax^{2}-(3a+1)x+3(a≠0) $,下列说法正确的是 ( )

A.点(1,2)在该函数的图象上
B.当 $ a= 1 $ 且 $-1\leqslant x\leqslant3$ 时,$0\leqslant y\leqslant8$
C.该函数的图象与 $ x $ 轴一定有交点
D.当 $ a＞0 $ 时,该函数图象的对称轴一定在直线 $ x= \frac{3}{2} $ 的左侧

答案： C

7. 已知 $ m＞n＞0 $,若关于 $ x $ 的方程 $ x^{2}+2x-3-m= 0 $ 的解为 $ x_{1},x_{2}(x_{1}＜x_{2}) $,关于 $ x $ 的方程 $ x^{2}+2x-3-n= 0 $ 的解为 $ x_{3},x_{4}(x_{3}＜x_{4}) $. 则下列结论正确的是 ( )

A.$ x_{3}＜x_{1}＜x_{2}＜x_{4} $
B.$ x_{1}＜x_{3}＜x_{4}＜x_{2} $
C.$ x_{1}＜x_{2}＜x_{3}＜x_{4} $
D.$ x_{3}＜x_{4}＜x_{1}＜x_{2} $

答案： B

8. 已知二次函数 $ y= ax^{2}+bx+c(a＜0) $ 的图象与 $ x $ 轴的一个交点坐标为 $(-1,0)$,对称轴为直线 $ x= 1 $,有下列结论:① $ a-b+c= 0 $;② 若点 $(-3,y_{1}),(2,y_{2}),(4,y_{3})$ 均在该二次函数图象上,则 $ y_{1}＜y_{2}＜y_{3} $;③ 若 $ m $ 为任意实数,则 $ am^{2}+bm+c\leqslant-4a $;④ 方程 $ ax^{2}+bx+c+1= 0 $ 的两实数根为 $ x_{1},x_{2} $,且 $ x_{1}＜x_{2} $,则 $ x_{1}＜-1 $,$ x_{2}＞3 $. 正确结论的序号为 ( )

A.①②③
B.①③④
C.②③④
D.①④

答案： B

9. 规定:如果两个函数的图象关于 $ y $ 轴对称,那么称这两个函数互为“Y 函数”. 例如:函数 $ y= x+3 $ 与 $ y= -x+3 $ 互为“Y 函数”. 若函数 $ y= \frac{k}{4}x^{2}+(k-1)x+k-3 $ 的图象与 $ x $ 轴只有一个交点,则它的“Y 函数”图象与 $ x $ 轴的交点坐标为 ______.

答案： (3,0)或(4,0)

10. 如图,二次函数 $ y= ax^{2}+bx+c $($ a,b,c $ 为常数,$ a≠0 $)的图象与 $ x $ 轴相交于点 $ A(-\frac{3}{2},0) $,对称轴是直线 $ x= -\frac{1}{2} $,有以下结论:① $ abc＜0 $;② 若点 $(-1,y_{1})$ 和点 $(2,y_{2})$ 都在抛物线上,则 $ y_{1}＜y_{2} $;③ $ am^{2}+bm\leqslant\frac{1}{4}a-\frac{1}{2}b $($ m $ 为任意实数);④ $ 3a+4c= 0 $. 其中正确的是 ( )


A.①②
B.③④
C.②③④
D.④

答案： B