《2025年全效学习课时提优九年级数学全一册人教版精华版》

10. 如图,⊙O 的半径为 7,AB 是⊙O 的弦,点 P 在弦 AB 上. 若 PA= 4,PB= 6,则 OP 的长为 ( )

A.$\sqrt{14}$
B.4
C.$\sqrt{23}$
D.5

答案： D

11. 沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”。如图,$\overset{\frown}{AB}$是以点 O 为圆心,OA 为半径的圆弧,C 是弦 AB 的中点,点 D 在$\overset{\frown}{AB}$上,CD⊥AB. “会圆术”给出$\overset{\frown}{AB}$长 l 的近似值 s 的计算公式$s = AB + \frac{CD^{2}}{OA}$,当 OA= 2,∠AOB= 90°时,|l - s|= ______(结果保留一位小数).

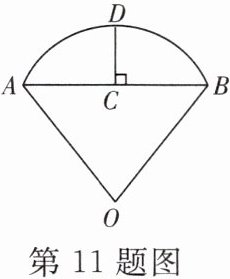
答案： 0.1

12. 只用一张矩形纸条和刻度尺,如何测量一次性纸杯杯口的直径？小聪同学所在的学习小组想到了如下方法：如图,将纸条拉直紧贴在杯口上,纸条的上下边沿分别与杯口相交于 A,B,C,D 四点,利用刻度尺量得该纸条宽为 3.5 cm,AB= 3 cm,CD= 4 cm,则可以算得纸杯的直径为 ______cm.

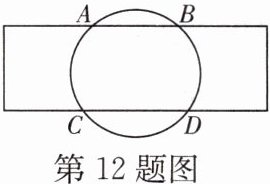
答案： 5

13. 某居民小区一处圆柱形的输水管道破裂,维修人员为了更换管道,需要确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
(1)请你补全这个输水管道的圆形截面(保留作图痕迹)；
(2)若这个输水管道有水部分的水面宽 AB= 16 cm,水的最大深度为 4 cm,求这个圆形截面的半径.

答案：
(1)略
(2)10 cm

14. 如图,⊙O 中两条相等且互相垂直的弦 AB,CD 相交于点 E.
(1)过点 O 作 OM⊥CD 于点 M,若 OM= 6,⊙O 的半径为 10,求弦 CD 的长；
(2)过点 A 作 AN⊥BD,交 CD 于点 F,求证：CE= EF.

答案：
(1)16
(2)略

15. [应用意识]如图,小明要帮助船夫计算一艘货船是否能够安全通过一座圆弧形的拱桥,现测得桥下水面 AB 宽 16 m,拱顶高出水平面(即 CD)4 m,货船宽 9 m,船舱顶部为矩形且高出水面 3 m.
(1)请你帮助小明求此圆弧形拱桥的半径；
(2)小明在解决这个问题时遇到困难,请你判断一下,此货船能顺利通过这座拱桥吗？说说你的理由.

答案：
(1)10 m
(2)不能.理由略