《2025年全效学习课时提优九年级数学全一册人教版精华版》

9. 如图,在平面直角坐标系中,若△ABC与$△A_1B_1C_1$关于点E成中心对称,点A,B,C的对应点分别为$A_1,B_1,C_1,$则对称中心点E的坐标是( )


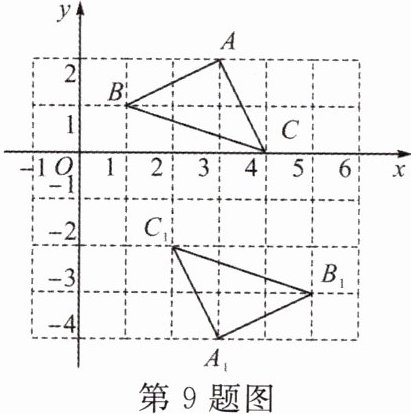
A.(3,-1)
B.(0,0)
C.(2,-1)
D.(-1,3)

答案： A

10. 如图,△ABC和△DEC关于点C成中心对称.若AC= 1,AB= 2,∠BAC= 90°,则AE的长为______.

答案： $2\sqrt{2}$

11. 如图,△ABO与△CDO关于点O成中心对称,点E,F在线段AC上,且AF= CE.求证：DF= BE.

答案：
∵△ABO与△CDO关于点O成中心对称，
∴OA=OC，OB=OD，∠AOB=∠COD。
∵AF=CE，OA=OC，
∴OA - AF = OC - CE，即OF=OE。
在△DOF和△BOE中，
OD=OB，
∠DOF=∠BOE（对顶角相等），
OF=OE，
∴△DOF≌△BOE（SAS）。
∴DF=BE。

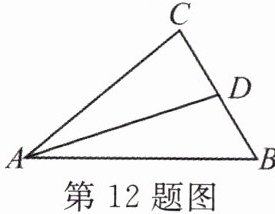
12. 如图,已知AD是△ABC的中线.
(1)画出以点D为对称中心,与△ABC成中心对称的三角形；
(2)若AB= 6 cm,AC= 4 cm,求AD长的取值范围.

答案：
(1)略
(2)1 cm＜AD＜5 cm

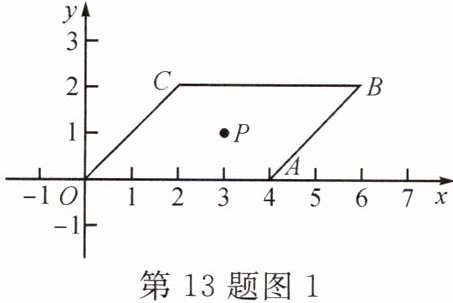
13. [推理能力]如图1,在平面直角坐标系中,□OABC的顶点A的坐标为(4,0),B的坐标为(6,2).
(1)请直接写出□OABC的中心P的坐标：______；
(2)求出直线PA的解析式；
(3)试说明：不论k取何值,□OABC都被直线y= kx+1-3k分成面积相等的两部分；


拓展：
(4)如图2,在平面直角坐标系中,□ABCD的边BC在x轴上,点A(0,3),B(-1,0).若直线y= -2x+4恰好平分□ABCD的面积,则点D的坐标为______；


(5)把8个边长为1的正方形按如图3所示的方式摆放在平面直角坐标系中,经过原点O的直线l将这8个正方形分成面积相等的两部分,则该直线l的函数解析式为______.

答案：
(1)(3,1)
(2)$y=-x+4$
(3)略
(4)$\left(\frac{7}{2},3\right)$
(5)$y=\frac{9}{10}x$