第17页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
9. 在煎炸臭豆腐时,我们把焦脆而不糊的豆腐块数占总数的百分比称为“可食用率”,在特定条件下,“可食用率”$p与煎炸的时间t$(单位:min)近似满足函数关系式:$p= at^{2}+bt+c$($a,b,c$为常数). 如图记录了三次实验数据,根据上述函数关系和实验数据,可以得到煎炸臭豆腐的最佳时间为 ( )
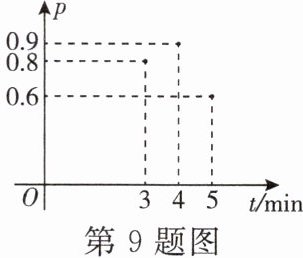
A.3.50 min
B.3.75 min
C.4.05 min
D.4.25 min

A.3.50 min
B.3.75 min
C.4.05 min
D.4.25 min
答案:
B
10. 抛物线$y= ax^{2}+bx+c上的部分点的横坐标x$,纵坐标$y$的对应值如下表:
| $x$ | $-2$ | $-1$ | $0$ | $1$ |
| $y$ | $0$ | $4$ | $6$ | $6$ |
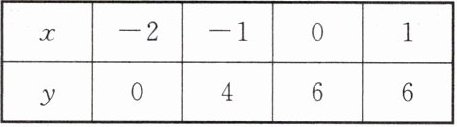
下列结论不正确的是 ( )
A.抛物线的开口向下
B.抛物线的对称轴是直线$x= \frac{1}{2}$
C.抛物线与x轴的一个交点坐标为$(2,0)$
D.函数$y= ax^{2}+bx+c的最大值为\frac{25}{4}$
| $x$ | $-2$ | $-1$ | $0$ | $1$ |
| $y$ | $0$ | $4$ | $6$ | $6$ |

下列结论不正确的是 ( )
A.抛物线的开口向下
B.抛物线的对称轴是直线$x= \frac{1}{2}$
C.抛物线与x轴的一个交点坐标为$(2,0)$
D.函数$y= ax^{2}+bx+c的最大值为\frac{25}{4}$
答案:
C
11. 在平面直角坐标系中,设函数$y= ax^{2}+bx+1$($a,b$是常数,$a\neq 0$).
(1)若该函数的图象经过$(1,0)和(2,1)$两点,求函数的解析式,并写出该函数图象的顶点坐标;
(2)已知$a= b= 1$,当$x= p,q$($p,q$是实数,$p\neq q$)时,该函数对应的函数值分别为$P,Q$. 若$p+q= 2$,求证:$P+Q>6$.
(1)若该函数的图象经过$(1,0)和(2,1)$两点,求函数的解析式,并写出该函数图象的顶点坐标;
(2)已知$a= b= 1$,当$x= p,q$($p,q$是实数,$p\neq q$)时,该函数对应的函数值分别为$P,Q$. 若$p+q= 2$,求证:$P+Q>6$.
答案:
(1)$y=x^{2}-2x+1$,顶点坐标为$(1,0)$
(2)略
(1)$y=x^{2}-2x+1$,顶点坐标为$(1,0)$
(2)略
12. 在平面直角坐标系$xOy$中,抛物线$y= ax^{2}-4ax-2(a<0)$与y轴相交于点$A$.
(1)求点$A$的坐标及抛物线的对称轴;
(2)当$-1\leqslant x\leqslant 4$时,$y$的最大值是2. 求当$-1\leqslant x\leqslant 4$时,$y$的最小值.
(1)求点$A$的坐标及抛物线的对称轴;
(2)当$-1\leqslant x\leqslant 4$时,$y$的最大值是2. 求当$-1\leqslant x\leqslant 4$时,$y$的最小值.
答案:
(1)点A坐标为$(0,-2)$,对称轴为直线$x=2$
(2)-7
(1)点A坐标为$(0,-2)$,对称轴为直线$x=2$
(2)-7
13. [创新意识]我们知道,经过原点的抛物线的解析式可以设为$y= ax^{2}+bx(a\neq 0)$. 对于这样的抛物线:
(1)当顶点坐标为$(1,1)$时,求$a,b$的值;
(2)当顶点坐标为$(m,2m)(m\neq 0)$时,求$a与m$之间的关系式;
(3)继续探究,如果$b\neq 0$,且抛物线的顶点在直线$y= (k+1)x(k\neq -1)$上,请用含$k的代数式表示b$.
(1)当顶点坐标为$(1,1)$时,求$a,b$的值;
(2)当顶点坐标为$(m,2m)(m\neq 0)$时,求$a与m$之间的关系式;
(3)继续探究,如果$b\neq 0$,且抛物线的顶点在直线$y= (k+1)x(k\neq -1)$上,请用含$k的代数式表示b$.
答案:
(1)$a=-1,b=2$
(2)$a=-\frac {2}{m}$
(3)$b=2k+2$
(1)$a=-1,b=2$
(2)$a=-\frac {2}{m}$
(3)$b=2k+2$
查看更多完整答案,请扫码查看


