第40页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
一 巧作辅助线
【教材母题1】(教材P87思考)
圆内接四边形的四个角之间有什么关系?
【思想方法】通过添加辅助线来构造圆心角或圆周角是实现圆内角度转换的有效手段,尤其要注意构造直径所对的圆周角.
【教材母题1】(教材P87思考)
圆内接四边形的四个角之间有什么关系?
【思想方法】通过添加辅助线来构造圆心角或圆周角是实现圆内角度转换的有效手段,尤其要注意构造直径所对的圆周角.
答案:
对角互补
【变式】(改变条件为内接三角形)
1. 如图,△ABC是⊙O的内接三角形,$AB= BC$,$\angle BAC= 30^\circ$,$AD$是直径.若$AD= 8$,则$AC$的长为 ( )
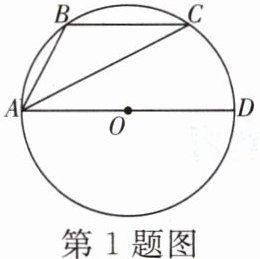
A.4
B.$4\sqrt{3}$
C.$\frac{8}{3}\sqrt{3}$
D.$2\sqrt{3}$
1. 如图,△ABC是⊙O的内接三角形,$AB= BC$,$\angle BAC= 30^\circ$,$AD$是直径.若$AD= 8$,则$AC$的长为 ( )

A.4
B.$4\sqrt{3}$
C.$\frac{8}{3}\sqrt{3}$
D.$2\sqrt{3}$
答案:
B
二 圆周角定理与垂径定理的综合运用
【教材母题2】(教材P89习题24.1第5题)
如图,在⊙O中,$OA\perp BC$,$\angle AOB= 50^\circ$.求$\angle ADC$的度数.
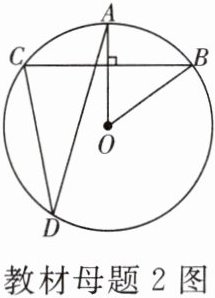
【思想方法】垂径定理与圆周角定理的综合运用题一般是通过圆周角定理进行角度转换,再利用垂径定理求解.
【教材母题2】(教材P89习题24.1第5题)
如图,在⊙O中,$OA\perp BC$,$\angle AOB= 50^\circ$.求$\angle ADC$的度数.

【思想方法】垂径定理与圆周角定理的综合运用题一般是通过圆周角定理进行角度转换,再利用垂径定理求解.
答案:
25°
【变式1】(改变图形,变求角度为求弦长)
2. 如图,⊙O为锐角三角形ABC的外接圆,其半径为5.
(1)用尺规作图作出$\angle BAC$的平分线,并标出它与劣弧BC的交点E(保留作图痕迹,不写作法);
(2)若(1)中的点E到弦BC的距离为3,求弦CE的长.
2. 如图,⊙O为锐角三角形ABC的外接圆,其半径为5.
(1)用尺规作图作出$\angle BAC$的平分线,并标出它与劣弧BC的交点E(保留作图痕迹,不写作法);
(2)若(1)中的点E到弦BC的距离为3,求弦CE的长.
答案:
(1)略
(2)$\sqrt{30}$
(1)略
(2)$\sqrt{30}$
【变式2】(变为圆周角定理的推论的运用)
3. 如图,AB是⊙O的直径,弦$CD\perp AB$于点E,G是$\widehat{AC}$上任意一点,连接AD,AG,GD.
(1)求证:$\angle ADC= \angle AGD$;
(2)若$BE= 2$,$CD= 8$,求⊙O的半径.
3. 如图,AB是⊙O的直径,弦$CD\perp AB$于点E,G是$\widehat{AC}$上任意一点,连接AD,AG,GD.
(1)求证:$\angle ADC= \angle AGD$;
(2)若$BE= 2$,$CD= 8$,求⊙O的半径.
答案:
(1)略
(2)5
(1)略
(2)5
查看更多完整答案,请扫码查看


