《2025年全效学习课时提优九年级数学全一册人教版精华版》

12. 如图,蒙古包可近似看作由圆锥和圆柱组成. 若用毛毡搭建一个底面圆面积为$25π m^2,$圆柱高为 3 m,圆锥高为 2 m 的蒙古包,则需要毛毡的面积为( )


A.$(30+5\sqrt{29})\pi\ m^2$
$B.40π m^2$
C.$(30+5\sqrt{21})\pi\ m^2$
$D.55π m^2$

答案： A

13. 如图,在矩形纸片 ABCD 中,AD= 6 cm,若把它分割成正方形纸片 ABFE 和矩形纸片 EFCD 后,分别裁出扇形 BAF 和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则 AB 的长为( )


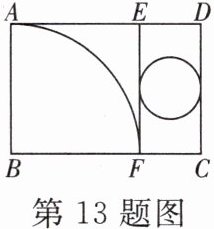
A.3.5 cm
B.4 cm
C.4.5 cm
D.5 cm

答案： B

14. 如图是一张平行四边形纸片 ABCD,BC= 36 cm,∠A= 110°,∠BDC= 50°,M 为 BC 的中点,若以点 M 为圆心,MC 长为半径画弧,交对角线 BD 于点 N,则∠NMC= ______°；将扇形 MCN 纸片剪下来围成一个无底盖的圆锥(接缝处忽略不计),则这个圆锥的底面圆半径为______ cm.

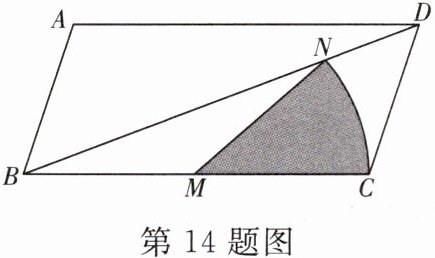
答案： 40 2

15. 如图,在半径为$\sqrt{2}$的圆形纸片中,剪一个圆心角为 90°的最大扇形(阴影部分).
(1)求这个扇形的面积；
(2)若将此扇形围成一个无底的圆锥(不计接头),求圆锥的底面半径.

答案：
(1)$\pi$
(2)$\frac{1}{2}$

16. 如图,在△ABC 中,AB= 4,AC= 2$\sqrt{2}$,∠B= 30°,0°＜∠C＜90°.
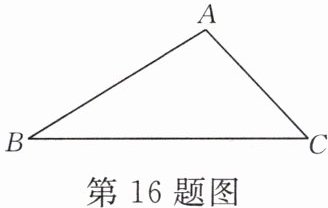
(1)求点 A 到直线 BC 的距离以及 BC 的长；
(2)将△ABC 绕线段 BC 所在直线旋转一周,求所得几何体的表面积.

答案：
(1)$2\sqrt{3}+2$
(2)$(8+4\sqrt{2})\pi$

17. [空间观念]如图,在等腰三角形 ABC 中,∠BAC= 120°,∠BAC 的平分线交 BC 于点 D,AD= 6,以点 A 为圆心,AD 长为半径画$\widehat{EF}$,交 AB 于点 E,交 AC 于点 F.
(1)求由$\widehat{EF}$及线段 FC,CB,BE 围成图形(阴影部分)的面积；
(2)将阴影部分剪掉,余下扇形 AEF,将扇形 AEF 围成一个圆锥的侧面,AE 与 AF 正好重合,求这个圆锥的高 h.

答案：
(1)$36\sqrt{3}-12\pi$
(2)$4\sqrt{2}$