第41页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
1. 如图,在⊙O中,AE是直径,点B在⊙O上,半径$OC\perp AB$于点D,连接BE.若$AB= 2\sqrt{7}$,$CD= 1$,则BE的长为 ( )
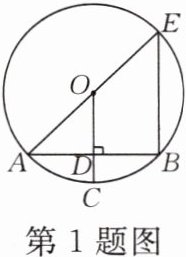
A.5
B.6
C.7
D.8

A.5
B.6
C.7
D.8
答案:
B
2. 如图,AB是圆的直径,$\angle 1$,$\angle 2$,$\angle 3$,$\angle 4$的顶点均在AB上方的圆弧上,$\angle 1$,$\angle 4$的一边分别经过点A,B,则$\angle 1+\angle 2+\angle 3+\angle 4= $______°.
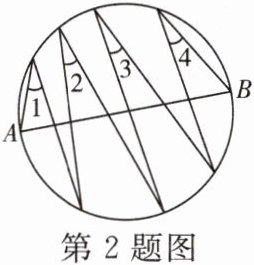

答案:
90
3. 如图,AB是⊙O的直径,弦$CD\perp AB$于点E.若$CD= 8$,$\angle D= 60^\circ$,则点A,C之间的距离为______,⊙O的半径为______.
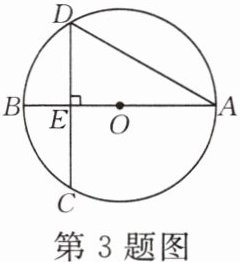

答案:
8 $\frac{8\sqrt{3}}{3}$
4. 如图,在△ABC中,$AB= AC$,以AB为直径作⊙O,交BC边于点D,交CA的延长线于点E,连接AD,DE.
(1)求证:$BD= CD$;
(2)若$AB= 5$,$DE= 4$,求AD的长.
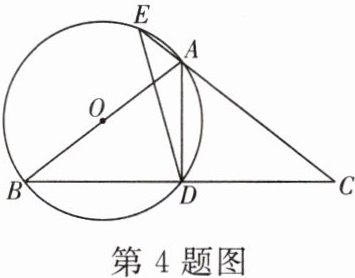
(1)求证:$BD= CD$;
(2)若$AB= 5$,$DE= 4$,求AD的长.

答案:
(1)略
(2)3
(1)略
(2)3
5. 已知阿基米德折弦定理:如图1,AB和BC是⊙O的两条弦(即折线ABC是圆的一条折弦),$BC>AB$,M是$\widehat{ABC}$的中点.若从点M向BC所作垂线的垂足为D,则D是折弦ABC的中点,即$CD= AB+BD$.
下面是运用“截长法”证明$CD= AB+BD$的部分证明过程.
证明:如图2,在CB上截取$CG= AB$,连接MA,MB,MC和MG.
∵M是$\widehat{ABC}$的中点,
∴$MA= MC$.
……
任务:(1)请按照上面的证明思路,写出该证明过程的剩余部分;
(2)填空:如图3,已知等边三角形ABC内接于⊙O,$AB= 2$,D是$\widehat{AC}$上一点,$\angle ABD= 45^\circ$,$AE\perp BD$于点E,则△BDC的周长为______.
 [img][img]
[img][img]
下面是运用“截长法”证明$CD= AB+BD$的部分证明过程.
证明:如图2,在CB上截取$CG= AB$,连接MA,MB,MC和MG.
∵M是$\widehat{ABC}$的中点,
∴$MA= MC$.
……
任务:(1)请按照上面的证明思路,写出该证明过程的剩余部分;
(2)填空:如图3,已知等边三角形ABC内接于⊙O,$AB= 2$,D是$\widehat{AC}$上一点,$\angle ABD= 45^\circ$,$AE\perp BD$于点E,则△BDC的周长为______.
 [img][img]
[img][img]
答案:
(1)略
(2)$2+2\sqrt{2}$
(1)略
(2)$2+2\sqrt{2}$
查看更多完整答案,请扫码查看


