《2025年学习质量监测九年级数学上册人教版》

5. 某村产业合作社种植了“千亩桃园”。销售前对本地市场进行调查发现：当批发价为4千元/吨时,每天可售出12吨,每吨每涨1千元,每天销量将减少2吨。据测算,每吨平均投入成本2千元,为了抢占市场,薄利多销,该村产业合作社决定,批发价每吨不低于4千元,不高于5.5千元。请解答以下问题：
(1)求每天获得的利润$y$(单位：千元)与批发价$x$(单位：千元/吨)之间的函数解析式,并直接写出自变量$x$的取值范围；
(2)当批发价为5千元/吨时,求出每天获得的利润。

答案：
(1)
由题意知，销量与批发价的关系为：销量 $= 12 - 2(x - 4)$。
每吨的利润为：$x - 2$（因为成本是2千元/吨）。
所以，总利润 $y$ 为：
$y = [12 - 2(x - 4)](x - 2)$
$= (12 - 2x + 8)(x - 2)$
$= (20 - 2x)(x - 2)$
$= -2x^2 + 24x - 40$。
根据题意，批发价 $x$ 的范围是 $4 \leq x \leq 5.5$。
所以，函数解析式为：$y = -2x^2 + 24x - 40 \quad (4 \leq x \leq 5.5)$。
(2)
将 $x = 5$ 代入 $y = -2x^2 + 24x - 40$，得到：
$y = -2(5^2) + 24(5) - 40$
$= -50 + 120 - 40$
$= 30$（千元）
所以，当批发价为5千元/吨时，每天获得的利润为30千元。

6. 某种火箭的飞行高度$h$(单位：$m$)关于发射后的飞行时间$t$(单位：$s$)的函数解析式为$h= -10t^{2}+200t$。
(1)发射后$t = 12$ $s$时,求火箭的飞行高度$h$的值。
(2)发射后$t$等于多少

秒

时

,火箭的高度为750m？
(3)发射后$t$等于多少秒时,火箭落回地面？

答案：
(1)
当$t = 12s$时，
将$t=12$代入$h=-10t^{2}+200t$中，
$h = -10×12^{2}+200×12$
$=-10×144 + 2400$
$=-1440+2400$
$= 960(m)$
(2)
当$h = 750m$时，
$-10t^{2}+200t=750$，
方程两边同时除以$-10$得：
$t^{2}-20t = - 75$，
移项得$t^{2}-20t + 75=0$，
对于一元二次方程$ax^{2}+bx+c=0(a\neq0)$，这里$a = 1$，$b=-20$，$c = 75$，
根据求根公式$t=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$，
$\Delta=b^{2}-4ac=(-20)^{2}-4×1×75=400 - 300 = 100$，
$t=\frac{20\pm\sqrt{100}}{2}=\frac{20\pm10}{2}$，
$t_{1}=\frac{20 + 10}{2}=15$，$t_{2}=\frac{20 - 10}{2}=5$。
(3)
当火箭落回地面时，$h = 0$，
即$-10t^{2}+200t=0$，
提取公因式$-10t$得：$-10t(t - 20)=0$，
则$-10t=0$或$t - 20=0$，
解得$t_{1}=0$（发射时的时刻，舍去），$t_{2}=20$。
综上：
(1)发射后$t = 12s$时，火箭的飞行高度$h$的值为$960m$；
(2)发射后$t$等于$5s$或$15s$时，火箭的高度为$750m$；
(3)发射后$t$等于$20s$时，火箭落回地面。

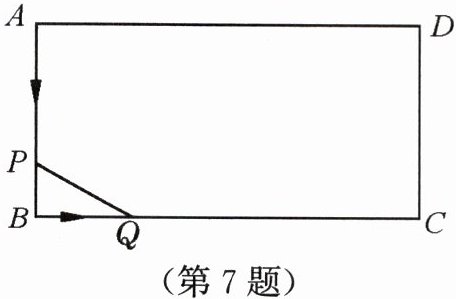
7. 如图,在矩形$ABCD$中,$AB = 10$ $cm$,$BC = 20$ $cm$,$P$,$Q两点同时从点A$出发,分别以1 $cm/s$和2 $cm/s的速度沿A→B→C→D→A$运动。当点$Q回到点A$时,$P$,$Q$两点立即停止运动,设点$P$,$Q运动的时间为t$ $s$。当$P$,$Q两点分别在AB边和BC$边上运动时,设以$P$,$B$,$Q为顶点的三角形的面积为S$ $cm^{2}$,请写出$S关于t的函数解析式及自变量t$的取值范围。

答案： 解：
1. 确定t的取值范围
点P在AB边上运动：AB=10cm，速度1cm/s，运动时间为$0 \leq t \leq 10$。
点Q在BC边上运动：Q先沿AB运动，AB=10cm，速度2cm/s，需$10÷2=5$s到达B点；再沿BC运动，BC=20cm，需$20÷2=10$s，故Q在BC边上的时间为$5 \leq t \leq 15$。
综上，P在AB边且Q在BC边时，$5 \leq t \leq 10$。
2. 计算PB和BQ的长度
$AP = 1 \cdot t = t$，则$PB = AB - AP = 10 - t$（cm）。
Q在BC边上运动的距离：$BQ = 2(t - 5)$（cm）（Q从B点开始运动时间为$t - 5$，速度2cm/s）。
3. 求三角形面积S
$PB \perp BQ$（矩形中AB⊥BC），故$S = \frac{1}{2} \cdot PB \cdot BQ$。
代入得：$S = \frac{1}{2}(10 - t) \cdot 2(t - 5) = (10 - t)(t - 5) = -t^2 + 15t - 50$。
函数解析式：$S = -t^2 + 15t - 50$
自变量取值范围：$5 \leq t \leq 10$