《2025年学习质量监测九年级数学上册人教版》

9. 一个等腰三角形的底边长比底边上的高少2,面积为60,则这个等腰三角形的周长为36.

答案： 36

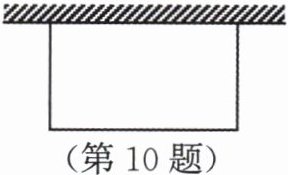
10. 如图,利用墙的一边,再用长为26m的铁丝网作三边,围成一个面积为$80m^2$的矩形养鸡场,若墙长为15m,则养鸡场的长和宽分别为10m和8m.

答案： 10，8

11. 将一块正方形铁皮的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,已知盒子的容积为$300cm^3,$求原铁皮的边长.

答案： 解：设原铁皮的边长为$x\,cm$。
由题意，剪去四角后做成的无盖盒子底面边长为$(x - 2×3)\,cm$，即$(x - 6)\,cm$，高为$3\,cm$。
盒子容积公式为：底面积$×$高，可得方程：
$(x - 6)^2 × 3 = 300$
化简方程：
$(x - 6)^2 = 100$
开平方得：
$x - 6 = \pm10$
解得：
$x_1 = 16$，$x_2 = -4$（边长不能为负，舍去）
答：原铁皮的边长为$16\,cm$。

12. 在美术馆里,张红看到一幅古典名画镶嵌在一个四周宽度相同的画框内,占据了墙面上很大的一块地方.如果这幅名画的长为20cm、高为30cm,在墙面上所占的面积为$3000cm^2,$那么这幅画的画框的宽度为多少?

答案： 设画框的宽度为$x\,cm$。
由题意，画框四周宽度相同，故包含画框的大矩形长为$(20 + 2x)\,cm$，高为$(30 + 2x)\,cm$，其面积为$3000\,cm^2$，可得方程：
$(20 + 2x)(30 + 2x) = 3000$
展开并化简：
$4x^2 + 100x + 600 = 3000$
$4x^2 + 100x - 2400 = 0$
$x^2 + 25x - 600 = 0$
解方程$x^2 + 25x - 600 = 0$，判别式$\Delta = 25^2 - 4 × 1 × (-600) = 3025$，
$x = \frac{-25 \pm \sqrt{3025}}{2} = \frac{-25 \pm 55}{2}$
解得$x_1 = 15$，$x_2 = -40$（宽度不能为负，舍去）。
答：画框的宽度为$15\,cm$。

1. 如图,某小区有一块长为18m,宽为6m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为$60m^2,$两块绿地之间及周边留有宽度相等的人行通道.若设人行通道的宽度为xm,则可以列出关于x的方程是(C).

A.$x^{2}+9x - 8 = 0$
B.$x^{2}-9x - 8 = 0$
C.$x^{2}-9x + 8 = 0$
D.$2x^{2}-9x + 8 = 0$
]

答案： C

2. 已知三角形两边的长分别是4和3,第三边的长是一元二次方程$x^{2}-8x + 15 = 0$的一个实数根,则该三角形的面积是(B).
A.12或$4\sqrt{5}$
B.6或$2\sqrt{5}$
C.6
D.$2\sqrt{5}$

答案： B

3. 一个菱形水池,它的两条对角线长的差为2m,水池的边长都是5m,则这个菱形水池的面积为24$m^2.$

答案： 24

4. 如图,有一张长40cm、宽25cm的长方形硬纸片,裁去角上四个小正方形之后,折成无盖纸盒.若纸盒的底面积是$450cm^2,$则纸盒的高是5cm.
]

答案： 5