《2025年学习质量监测九年级数学上册人教版》

5. 某商场将进货价为45元的某种服装以65元售出,平均每天可售30件,由于季节的变换,为了尽快减少库存,商场决定采取适当的降价措施,调查发现：若每件降价1元,则每天可多售出5件.如果每天要盈利800元,每件应降价多少元?

答案： 设每件应降价$x$元。
原售价为65元，降价后售价为$(65 - x)$元。
原进货价为45元，因此降价后的单件利润为$(65 - x - 45)$元。
原每天销售量为30件，降价后每天销售量为$(30 + 5x)$件。
根据题意，每天盈利为800元，因此有方程：
$(65 - x - 45)(30 + 5x) = 800$
展开方程得：
$(20 - x)(30 + 5x) = 800$
进一步展开并整理得：
$600 + 100x - 30x - 5x^2 = 800$
整理为标准形式：
$5x^2 - 70x + 200 = 0$
除以5得：
$x^2 - 14x + 40 = 0$
因式分解得：
$(x - 4)(x - 10) = 0$
解得：
$x_1 = 4, \quad x_2 = 10$
由于题目要求尽快减少库存，因此选择降价更多的方案，即$x = 10$（当降价10元时，销售量增加更多，更符合减少库存的需求，且两个解都符合盈利800元的条件，但题目要求选择降价更多的，所以取$x=10$，若题目没有该要求，则两个解都可行）。
答：每件服装应降价10元（若没有减少库存的额外要求，则降价4元或10元均可）。

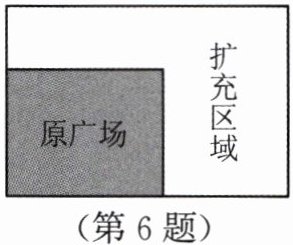
6. 某地计划对一矩形广场进行扩建改造.如图,原广场的长为50m、宽为40m,要求扩建后的矩形广场的长与宽的比为3:2.扩充区域的扩建费用为每平方米30元,扩建后在原广场和扩充区域都铺设地砖,铺设地砖的费用为每平方米100元.如果计划扩建改造的总费用为642000元,扩建后广场的长和宽应分别是多少米?
]

答案： 设扩建后广场的长为$3x$米，宽为$2x$米。
原广场面积：$50×40 = 2000$平方米。
扩建后总面积：$3x×2x = 6x²$平方米。
扩充区域面积：$6x² - 2000$平方米。
总费用=扩充区域扩建费用+铺设地砖费用，依题意得：
$30(6x² - 2000) + 100×6x² = 642000$
化简方程：
$180x² - 60000 + 600x² = 642000$
$780x² = 702000$
$x² = 900$
$x = 30$（$x=-30$舍去）
扩建后长：$3x = 90$米，宽：$2x = 60$米。
答：扩建后广场的长为90米，宽为60米。

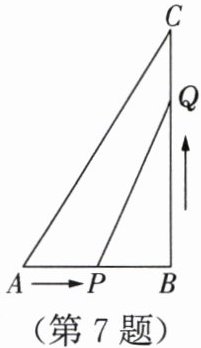
7. 如图,在△ABC中,∠B = 90°,AB = 5cm,BC = 8cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,同时点Q从点B开始沿BC边向点C以2cm/s的速度移动,当其中一点到达终点时,另外一点也随之停止运动.
(1)△PQB的面积能否等于$9cm^2? $请说明理由.
(2)几秒后,四边形APQC的面积等于$16cm^2? $请写出过程.
]

答案： （1）设运动时间为$ t $秒，其中$ 0 \leq t \leq 4 $（$ Q $先到达终点，$ t=4 $时运动停止）。
$ PB = AB - AP = 5 - t $，$ BQ = 2t $，$ \triangle PQB $面积$ S = \frac{1}{2} × PB × BQ = \frac{1}{2}(5 - t)(2t) = t(5 - t) $。
令$ t(5 - t) = 9 $，整理得$ t^2 - 5t + 9 = 0 $。
判别式$ \Delta = (-5)^2 - 4 × 1 × 9 = 25 - 36 = -11 ＜ 0 $，方程无实根。
故$ \triangle PQB $面积不能等于$ 9\ cm^2 $。
（2）$ S_{\triangle ABC} = \frac{1}{2} × 5 × 8 = 20\ cm^2 $，四边形$ APQC $面积$ = 20 - S_{\triangle PQB} $。
令$ 20 - t(5 - t) = 16 $，整理得$ t^2 - 5t + 4 = 0 $。
解得$ t_1 = 1 $，$ t_2 = 4 $，均满足$ 0 \leq t \leq 4 $。
故1秒或4秒后，四边形$ APQC $面积等于$ 16\ cm^2 $。
（1）不能；（2）1秒或4秒。