第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
一、计算。
$\frac{3}{8}+\frac{2}{7}÷\frac{3}{14}$
$\frac{4}{5}-9÷\frac{3}{10}×\frac{1}{60}$
$\frac{4}{5}÷(2-\frac{2}{3})$
$\frac{1}{6}×[\frac{14}{15}-(\frac{3}{5}+\frac{3}{10})]$
$\frac{3}{8}+\frac{2}{7}÷\frac{3}{14}$
$\frac{4}{5}-9÷\frac{3}{10}×\frac{1}{60}$
$\frac{4}{5}÷(2-\frac{2}{3})$
$\frac{1}{6}×[\frac{14}{15}-(\frac{3}{5}+\frac{3}{10})]$
答案:
一、计算。
1.
$\;\;\;\;\frac{3}{8} + \frac{2}{7} ÷ \frac{3}{14}$
$=\frac{3}{8} + \frac{2}{7} × \frac{14}{3}$
$=\frac{3}{8} + \frac{4}{3}$
$=\frac{9}{24} + \frac{32}{24}$
$= \frac{41}{24}$
2.
$\;\;\;\;\frac{4}{5} - 9 ÷ \frac{3}{10} × \frac{1}{60}$
$=\frac{4}{5} - 9 × \frac{10}{3} × \frac{1}{60}$
$=\frac{4}{5} - 30 × \frac{1}{60}$
$=\frac{4}{5} - \frac{1}{2}$
$=\frac{8}{10} - \frac{5}{10}$
$= \frac{3}{10}$
3.
$\;\;\;\;\frac{4}{5} ÷ (2 - \frac{2}{3})$
$=\frac{4}{5} ÷ \frac{4}{3}$
$= \frac{4}{5} × \frac{3}{4}$
$= \frac{3}{5}$
4.
$\;\;\;\;\frac{1}{6} × [\frac{14}{15} - (\frac{3}{5} + \frac{3}{10})]$
$=\frac{1}{6} × [\frac{14}{15} - (\frac{6}{10} + \frac{3}{10})]$
$=\frac{1}{6} × [\frac{14}{15} - \frac{9}{10}]$
$=\frac{1}{6} × [\frac{28}{30} - \frac{27}{30}]$
$= \frac{1}{6} × \frac{1}{30}$
$= \frac{1}{180}$
1.
$\;\;\;\;\frac{3}{8} + \frac{2}{7} ÷ \frac{3}{14}$
$=\frac{3}{8} + \frac{2}{7} × \frac{14}{3}$
$=\frac{3}{8} + \frac{4}{3}$
$=\frac{9}{24} + \frac{32}{24}$
$= \frac{41}{24}$
2.
$\;\;\;\;\frac{4}{5} - 9 ÷ \frac{3}{10} × \frac{1}{60}$
$=\frac{4}{5} - 9 × \frac{10}{3} × \frac{1}{60}$
$=\frac{4}{5} - 30 × \frac{1}{60}$
$=\frac{4}{5} - \frac{1}{2}$
$=\frac{8}{10} - \frac{5}{10}$
$= \frac{3}{10}$
3.
$\;\;\;\;\frac{4}{5} ÷ (2 - \frac{2}{3})$
$=\frac{4}{5} ÷ \frac{4}{3}$
$= \frac{4}{5} × \frac{3}{4}$
$= \frac{3}{5}$
4.
$\;\;\;\;\frac{1}{6} × [\frac{14}{15} - (\frac{3}{5} + \frac{3}{10})]$
$=\frac{1}{6} × [\frac{14}{15} - (\frac{6}{10} + \frac{3}{10})]$
$=\frac{1}{6} × [\frac{14}{15} - \frac{9}{10}]$
$=\frac{1}{6} × [\frac{28}{30} - \frac{27}{30}]$
$= \frac{1}{6} × \frac{1}{30}$
$= \frac{1}{180}$
二、看图列式计算。
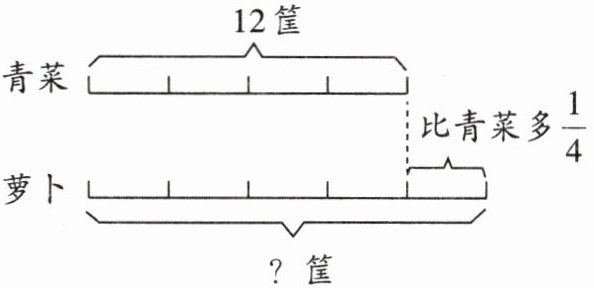
1.
2.
1.

2.

答案:
1.
解析:考查分数的应用,通过已知青菜的数量以及萝卜比青菜多的比例,求出萝卜的数量。
计算过程:萝卜比青菜多$\frac{1}{4}$,则萝卜的数量是青菜的$1 + \frac{1}{4}=\frac{5}{4}$。
已知青菜有$12$筐,所以萝卜的数量为$12×\frac{5}{4} = 15$(筐)。
答案:$12×(1 + \frac{1}{4}) = 15$(筐)。
2.
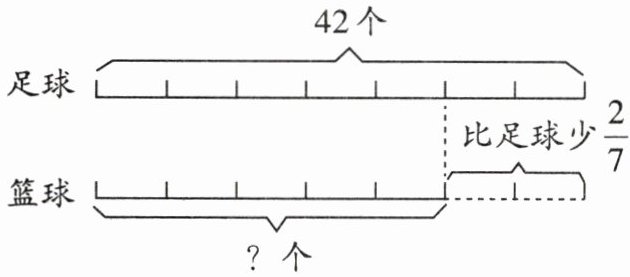
解析:考查分数的应用,根据足球的数量以及篮球比足球少的比例,求出篮球的数量。
计算过程:篮球比足球少$\frac{2}{7}$,那么篮球的数量是足球的$1 - \frac{2}{7}=\frac{5}{7}$。
已知足球有$42$个,所以篮球的数量为$42×\frac{5}{7} = 30$(个)。
答案:$42×(1 - \frac{2}{7}) = 30$(个)。
解析:考查分数的应用,通过已知青菜的数量以及萝卜比青菜多的比例,求出萝卜的数量。
计算过程:萝卜比青菜多$\frac{1}{4}$,则萝卜的数量是青菜的$1 + \frac{1}{4}=\frac{5}{4}$。
已知青菜有$12$筐,所以萝卜的数量为$12×\frac{5}{4} = 15$(筐)。
答案:$12×(1 + \frac{1}{4}) = 15$(筐)。
2.
解析:考查分数的应用,根据足球的数量以及篮球比足球少的比例,求出篮球的数量。
计算过程:篮球比足球少$\frac{2}{7}$,那么篮球的数量是足球的$1 - \frac{2}{7}=\frac{5}{7}$。
已知足球有$42$个,所以篮球的数量为$42×\frac{5}{7} = 30$(个)。
答案:$42×(1 - \frac{2}{7}) = 30$(个)。
三、解决问题。(只列式不计算)
1. 一根绳子长30米,剪去了$\frac{3}{5}$,还剩多少米?
2. 一根绳子长30米,剪去了一些后还剩$\frac{3}{5}$,还剩多少米?
3. 饲养场养鸡600只,鸭的只数比鸡少$\frac{1}{6}$。饲养场养了多少只鸭?
4. 饲养场养鸡600只,鹅的只数比鸡多$\frac{1}{6}$。饲养场养了多少只鹅?
1. 一根绳子长30米,剪去了$\frac{3}{5}$,还剩多少米?
2. 一根绳子长30米,剪去了一些后还剩$\frac{3}{5}$,还剩多少米?
3. 饲养场养鸡600只,鸭的只数比鸡少$\frac{1}{6}$。饲养场养了多少只鸭?
4. 饲养场养鸡600只,鹅的只数比鸡多$\frac{1}{6}$。饲养场养了多少只鹅?
答案:
1. 解析:本题考查的是分数的应用,需要剪去的长度占总长的比例来计算剩余长度。
答案:$30 × (1 - \frac{3}{5})$。
2. 解析:本题考查的是分数的应用,通过剩余长度占总长的比例来直接计算剩余长度。
答案:$30 × \frac{3}{5}$。
3. 解析:本题考查的是分数的应用,通过鸡的数量和鸭与鸡数量的比例关系来计算鸭的数量。
答案:$600 × (1 - \frac{1}{6})$。
4. 解析:本题考查的是分数的应用,通过鸡的数量和鹅与鸡数量的比例关系来计算鹅的数量。
答案:$600 × (1 + \frac{1}{6})$。
答案:$30 × (1 - \frac{3}{5})$。
2. 解析:本题考查的是分数的应用,通过剩余长度占总长的比例来直接计算剩余长度。
答案:$30 × \frac{3}{5}$。
3. 解析:本题考查的是分数的应用,通过鸡的数量和鸭与鸡数量的比例关系来计算鸭的数量。
答案:$600 × (1 - \frac{1}{6})$。
4. 解析:本题考查的是分数的应用,通过鸡的数量和鹅与鸡数量的比例关系来计算鹅的数量。
答案:$600 × (1 + \frac{1}{6})$。
四、小军从学校向文化馆走去,同时小辉沿同一条路从文化馆向学校走去。小军每分钟走$\frac{3}{20}$千米,小辉每分钟走$\frac{1}{10}$千米,10分钟后,小军和小辉相遇。学校到文化馆的路程有多少千米?
答案:
解析:本题考查的知识点是相遇问题。利用路程=速度×时间,先分别求出小军和小辉10分钟走的路程,再将二者相加,即可求出学校到文化馆的路程。
答案:
小军10分钟走的路程:
$\frac{3}{20}×10=\frac{3}{2}=1.5$(千米),
小辉10分钟走的路程:
$\frac{1}{10}×10=1$(千米),
学校到文化馆的路程:
$1.5+1=2.5$(千米),
所以学校到文化馆的路程有2.5千米。
答案:
小军10分钟走的路程:
$\frac{3}{20}×10=\frac{3}{2}=1.5$(千米),
小辉10分钟走的路程:
$\frac{1}{10}×10=1$(千米),
学校到文化馆的路程:
$1.5+1=2.5$(千米),
所以学校到文化馆的路程有2.5千米。
查看更多完整答案,请扫码查看


