《2025年新课程课堂同步练习册六年级数学上册苏教版》

一、直接写出得数。
$\frac{4}{11}×33=$12
$\frac{8}{17}×51=$24
$35×\frac{7}{25}=$$\frac{49}{5}$ (或者写成 $9.8$)
$64×\frac{15}{16}=$60

答案： 解析：
这些题目都是分数与整数的乘法运算。
对于这类题目，我们将分数与整数相乘，即分子与整数相乘，分母保持不变，然后化简得到结果。
答案：
$\frac{4}{11} × 33 = 12$
$\frac{8}{17} × 51 = 24$
$35 × \frac{7}{25} = \frac{49}{5}$ (或者写成 $9.8$)
$64 × \frac{15}{16} = 60$

二、计算。
$\frac{2}{3}×\frac{3}{5}÷\frac{2}{3}×\frac{3}{5}$
$\frac{4}{15}÷\left[\frac{3}{8}×\left(\frac{2}{3}-\frac{1}{9}\right)\right]$
$\frac{4}{7}×\frac{6}{5}+\frac{6}{7}÷\frac{5}{6}$

答案： 解析：这三道题目都是分数的四则运算。
第一题主要考查分数的乘除混合运算，需要注意运算顺序，从左到右依次计算，或者通过交换律和结合律简化计算。
第二题涉及到分数的四则运算和括号的使用，需要先算括号内的减法，再进行乘法和除法运算。
第三题则考查了分数的乘法和除法，以及分配律的应用，可以通过分配律简化计算。
答案：
第一题：
$\;\;\;\;\frac{2}{3} × \frac{3}{5} ÷ \frac{2}{3} × \frac{3}{5}$
$ = \frac{2}{3} × \frac{3}{5} × \frac{3}{2} × \frac{3}{5}$
$ = \frac{2 × 3 × 3 × 3}{3 × 5 × 2 × 5}$
$ = \frac{9}{25}$
第二题：
$\;\;\;\;\frac{4}{15} ÷ \left[ \frac{3}{8} × \left( \frac{2}{3} - \frac{1}{9} \right) \right]$
$ = \frac{4}{15} ÷ \left[ \frac{3}{8} × \frac{6-1}{9} \right]$
$ = \frac{4}{15} ÷ \left[ \frac{3}{8} × \frac{5}{9} \right]$
$ = \frac{4}{15} ÷ \frac{5}{24}$
$ = \frac{4}{15} × \frac{24}{5}$
$ = \frac{4 × 24}{15 × 5}$
$ = \frac{32}{25}$
第三题：
$\;\;\;\;\frac{4}{7} × \frac{6}{5} + \frac{6}{7} ÷ \frac{5}{6}$
$ = \frac{4}{7} × \frac{6}{5} + \frac{6}{7} × \frac{6}{5}$
$ = \frac{6}{5} × \left( \frac{4}{7} + \frac{6}{7} \right)$
$ = \frac{6}{5} × \frac{10}{7}$
$ = \frac{6 × 10}{5 × 7}$
$ = \frac{12}{7}$

三、看图列式计算。
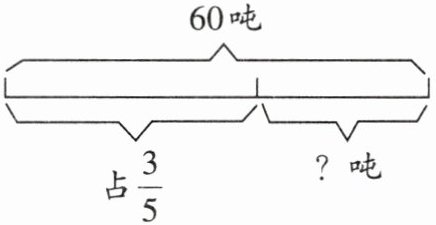
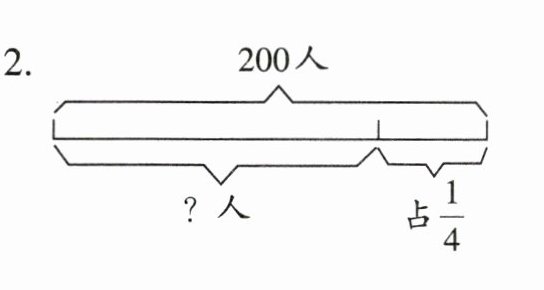
1.
2.

答案： 1. $60×(1-\frac{3}{5})=24$（吨）
2. $200×(1-\frac{1}{4})=150$（人）

1. 某校六(1)班有学生45人,其中女生占$\frac{2}{5}$。男生有多少人?

答案： 解析：本题考查的是分数乘法应用题，要求男生人数，需要先求出女生人数，再用总人数减去女生人数得到男生人数，或者先求出男生占总人数的比例，再用总人数乘以该比例得到男生人数。
答案：
方法一：
女生人数：$45×\frac{2}{5}=18$（人），
男生人数：$45 - 18 = 27$（人）。
方法二：
男生占总人数的比例：$1-\frac{2}{5}=\frac{3}{5}$，
男生人数：$45×\frac{3}{5}=27$（人）。
答：男生有27人。

2. 修一条长100千米的公路,已经修了$\frac{7}{10}$,还剩多少千米没修?

答案： 解析：题目考查稍复杂的分数乘法实际问题。要求出还剩多少千米没修，需要先求出没修的占全长的几分之几，再用全长乘以没修的占比即可。
答案：
已经修了$\frac{7}{10}$，则没修的为$1 - \frac{7}{10} = \frac{3}{10}$。
全长$100$千米，所以没修的长度为$100 × \frac{3}{10} = 30$（千米）。
答：还剩$30$千米没修。

五、小明家买回一袋重50千克的大米,第一周吃了$\frac{1}{10}$后,主动装了一些大米给不方便采购的邻居李大爷,此时还剩$\frac{1}{5}$。小明家送出了多少千克大米给李大爷?

答案： 解析：
本题考查的是分数的乘法和减法运算。
首先，需要计算小明家第一周吃了多少大米。
已知小明家买回的大米重量为50千克，第一周吃了总重量的$\frac{1}{10}$。
所以，第一周吃的大米重量为：
$50 × \frac{1}{10} = 5(千克)$
接着，需要计算第一周吃完后还剩下多少大米。
初始重量减去第一周吃的重量，即：
$50 - 5 = 45(千克)$
然后，计算小明家送出大米后剩下的大米重量。
已知送出后剩下的大米占总重量的$\frac{1}{5}$，所以剩下的大米重量为：
$50 × \frac{1}{5} = 10(千克)$ （注意，这里用初始重量50千克来计算，因为送出的是基于初始重量的部分）
但实际上，第一周后剩下45千克，送出后剩下10千克，所以送出的大米应该是第一周后的剩余量减去最后剩下的量。
最后，计算小明家送出了多少大米给李大爷。
第一周后的剩余量减去剩下的量，即送出的大米重量：
$45 - 10 = 35(千克)$
答案：
小明家送出了35千克大米给李大爷。