《2025年同步测控优化设计九年级数学上册人教版精编版》

1. 连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线。

答案： 母线

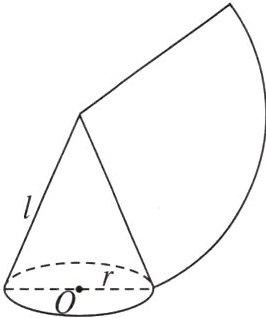
2. 如图,沿一条母线将圆锥侧面剪开并展平,圆锥的侧面展开图是一个扇形,设圆锥的母线长为$l$,底面圆的半径为$r$,那么这个扇形的半径为$l$,扇形的弧长为$2πr$,因此圆锥的侧面积为$πrl$,圆锥的全面积为$πrl+πr²$。

答案： 扇形　l　2πr　πrl　πrl+πr²

3. 已知圆锥的底面半径为$1\mathrm{cm}$,母线长为$9\mathrm{cm}$,则圆锥的全面积为(C)
A.$6\pi\mathrm{cm}^2$
B.$9\pi\mathrm{cm}^2$
C.$10\pi\mathrm{cm}^2$
D.$27\pi\mathrm{cm}^2$

答案： C

4. 若圆锥的底面半径为$\frac{1}{2}$,母线长为$2$,则它的侧面展开图的圆心角的度数为90°。

答案： 90°

1. 已知圆锥的底面半径为$4\mathrm{cm}$,高为$5\mathrm{cm}$,则它的表面积为(D)
A.$12\pi\mathrm{cm}^2$
B.$26\pi\mathrm{cm}^2$
C.$\sqrt{41}\pi\mathrm{cm}^2$
D.$(4\sqrt{41}+16)\pi\mathrm{cm}^2$

答案： D

2. 小刚用一张半径为$24cm$的扇形纸板做一个如图所示的圆锥形小丑帽子的侧面（接缝处忽略不计），如果做成的圆锥形小丑帽子的底面半径为$10cm$，那么这张扇形纸板的面积是（ ）

A. $120\pi\mathrm{cm}^2$
B. $240\pi\mathrm{cm}^2$
C. $260\pi\mathrm{cm}^2$
D. $480\pi\mathrm{cm}^2$

答案： B

3. 用半径为$3\mathrm{cm}$,圆心角是$120^{\circ}$的扇形围成一个圆锥的侧面,则这个圆锥的底面半径为(D)
A.$2\pi\mathrm{cm}$
B.$1.5\mathrm{cm}$
C.$\pi\mathrm{cm}$
D.$1\mathrm{cm}$

答案： D

4. 已知圆锥的侧面展开图的弧长为$6\pi\mathrm{cm}$,圆心角为$216^{\circ}$,则此圆锥的母线长为5$\mathrm{cm}$。

答案： 5

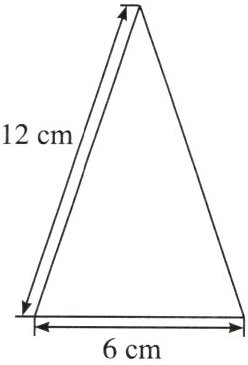
5. 右面是一个圆锥的轴截面,则此圆锥的侧面展开图的圆心角的度数为90°。

答案： 90°

6. 一个圆锥的高为$3$,侧面展开图是半圆,求：
(1)圆锥的母线与底面半径之比；
(2)圆锥的全面积。

答案：
解：如图，设圆锥的轴截面为△ABC，过A作AO⊥BC于点O，设母线长AB=l，底面⊙O的半径为r，高AO=h.
　　　　　　　
(1)
∵圆锥的侧面展开图是半圆，
∴2πr=$\frac{1}{2}$×2πl=πl，$\frac{l}{r}$=2.
(2)在Rt△ABO中，
∵l²=r²+h²，l=2r，h=3，
∴(2r)²=3²+r².
　　　由r为正数，解得r=$\sqrt{3}$，l=2r=2$\sqrt{3}$.
　　　故S全=S侧+S底=πrl+πr²=π×$\sqrt{3}$×2$\sqrt{3}$+π×($\sqrt{3}$)²=9π.