《2025年同步测控优化设计九年级数学上册人教版精编版》

1. 一般地,形如y=ax²+bx+c(a,b,c是常数,a≠0)的函数,叫做二次函数。其中,x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项。

答案： y=ax²+bx+c

2. 在圆的面积公式$S= πR^2$中,S与R之间的关系是(C)
A.S是R的正比例函数
B.S是R的一次函数
C.S是R的二次函数
D.以上答案都不对

答案： C

3. 二次函数的三个特征：
(1)函数解析式等号两边必须是整式；
(2)化简后自变量的最高次数必须是2；
(3)二次项系数必须不为0。

答案：
(1)整式
(2)2
(3)0

4. 若函数$y= (n-3)x^{n^2-7}+2x-1$是二次函数,则n=-3。

答案： -3

1. 下列函数中,是以x为自变量的二次函数的是(A)
A.y= $\frac{1}{2}$x(x-3)
$B.y= (x+2)(x-2)-(x-1)^2$
C.y= $\frac{1}{x^2+x-1}$
D.y= $\sqrt{x^2+2x-3}$

答案： A

2. 若某种商品原价为a元,经过两次降价后为y元,假设每次降价的百分率均为x,则y与x之间的函数解析式为(C)
A.$y= ax^2+a$
B.$y= x^2+a$
C.$ y= ax^2-2ax+a$
D.y= a-2x

答案： C

3. 已知二次函数$y= ax^2+bx-1(a≠0),$当x= 1时,y= 1,则代数式1-a-b的值为(B)
A.-3
B.-1
C.2
D.5

答案： B

4. 已知二次函数$y= 1-3x+5x^2,$则二次项系数a=5,一次项系数b= ______-3,常数项c= ______1。

答案： 5 -3 1

5. 已知正三角形的边长为x cm,面积为$y cm^2,$则y与x之间的函数解析式为y=√3/4x²,y是(填“是”或“不是”)x的二次函数。

答案： y=√3/4x² 是

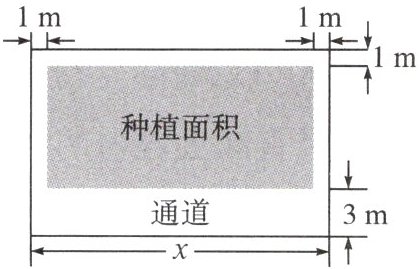
6. 小明的爸爸拟建一个温室大棚,小明帮助爸爸画出了它的平面图形,温室外围是一个矩形,周长为120 m,室内通道的尺寸如图所示,设大棚的一条边长为x(单位：m),种植面积为y(单位：$m^2),$为了能较容易地计算出种植面积,请你帮助小明建立一个能反映种植面积y与x的函数解析式。

答案： 分析 根据题图中标出的尺寸,得种植面积的一边长为(60-x-1-3)m,另一边长为(x-1-1)m,根据矩形面积公式即可求出 y 与 x 的函数解析式.解 y=(60-x-1-3)(x-1-1)=-x²+58x-112.