《2025年同步测控优化设计九年级数学上册人教版精编版》

1. 因为抛物线 $ y = ax^2 + bx + c $ 的顶点是最低(高)点,所以当 $ x = $$-\frac{b}{2a}$时,二次函数 $ y = ax^2 + bx + c $ 有最小(大)值$\frac{4ac-b^{2}}{4a}$.

答案： $-\frac{b}{2a}$ $\frac{4ac-b^{2}}{4a}$

2. 当 $ x = $____时,二次函数 $ y = x^2 + 2x - 2 $ 有最小值.

答案： -1

3. 利用二次函数求最大利润时,若列出的二次函数图象的对称轴恰好题目限定的自变量的范围内,则二次函数的最大值就是所要求的最大利润;当求得的二次函数图象的对称轴不在题目限定的自变量的范围内,我们先要搞清自变量的取值在对称轴左侧还是右侧,然后结合二次函数的增减性求出最大利润;当在不同的自变量取值范围内,函数表达式不同时,我们需要分段讨论,求出每种情况下的最大值,然后综合考虑.

答案： 大值 左 右 最大值

4. 某商店经营一种水产品,成本为40元/千克,据市场分析,若按50元/千克销售,一个月能售出500千克;销售价每涨1元,月销售量就减少10千克,针对这种水产品的销售情况,销售单价定为70元时,获得的利润最多.

答案： 70

1. 某公司准备修建一个长方体的污水处理池,若池底矩形的周长为100m,则池底的最大面积是(B)
A.$ 600m^2 $
B.$ 625m^2 $
C.$ 650m^2 $
D.$ 675m^2 $

答案： B

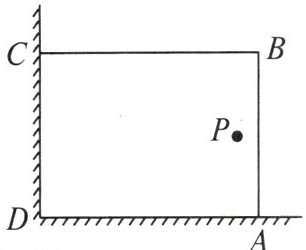
2. 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园 $ ABCD $(篱笆只围 $ AB $, $ BC $ 两边),设 $ AB = xm $. 若在 $ P $ 处有一棵树与墙 $ CD $, $ AD $ 的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),则花园面积 $ S $ 的最大值为(B)

A.$ 196m^2 $
B.$ 195m^2 $
C.$ 190m^2 $
D.$ 180m^2 $

答案： B

3. 老刘准备在某地投资修建一个有30个房间供旅客住宿的旅游度假村,并将其全部利润用于当地建设. 据测算,若每个房间的定价为60元/天,则房间将会住满;每个房间的定价每增加5元/天,就会有一个房间空闲. 度假村对旅客住宿的房间每间将支出各种费用20元/天(没住宿的不支出),当房价定为(C)元/天时,度假村的利润最大.
A.110
B.105
C.115
D.120

答案： C

4. 某商店销售一批头盔,售价为80元每顶,每月可售出200顶. 在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶. 已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为70元.

答案： 70

5. 某药店选购了一批消毒液,进价为每瓶10元,在销售过程中发现,每天销售量 $ y $(单位:瓶)与每瓶售价 $ x $(单位:元)之间存在一次函数关系(其中 $ 10 \leq x \leq 21 $,且 $ x $ 为整数). 当每瓶消毒液售价为12元时,每天销售量为90瓶;当每瓶消毒液售价为15元时,每天销售量为75瓶.
(1)求 $ y $ 与 $ x $ 之间的函数解析式;
(2)设该药店销售该消毒液每天的销售利润为 $ w $ 元,当每瓶消毒液售价为多少元时,药店销售该消毒液每天销售利润最大,最大利润是多少元?

答案： 解
(1)设y与x之间的函数解析式为y=kx+b(k≠0),将(12,90),(15,75)代入y=kx+b,得$\left\{\begin{array}{l} 12k+b=90,\\ 15k+b=75,\end{array}\right. $解得$\left\{\begin{array}{l} k=-5,\\ b=150,\end{array}\right. $所以y与x之间的函数解析式为y=-5x+150(10≤x≤21,且x为整数).
(2)依题意,得w=(x-10)·(-5x+150)=$-5x^{2}+200x-1500=-5(x-20)^{2}+500.$因为-5＜0,10≤x≤21,且x为整数,所以当x=20时,w取得最大值,最大值为500.答:当每瓶消毒液售价为20元时,药店销售该消毒液每天销售利润最大,最大利润是500元.