《2025年同步测控优化设计九年级数学上册人教版精编版》

4. 已知二次函数的图象经过点 $ A(0, - 3) $,$ B(2, - 3) $,$ C(-1, 0) $,则此二次函数的解析式是y=x²−2x−3,图象的顶点坐标是(1,−4).

答案： y=x²−2x−3　(1,−4)

1. 抛物线 $ y = x^{2} + 2x - 3 $ 的开口方向、顶点坐标分别是(A)
A.开口向上、顶点坐标为 $ (-1, - 4) $
B.开口向下、顶点坐标为 $ (1, 4) $
C.开口向上、顶点坐标为 $ (1, 4) $
D.开口向下、顶点坐标为 $ (-1, - 4) $

答案： A

2. 把二次函数 $ y = - \frac{1}{4}x^{2} - x + 3 $ 用配方法化成 $ y = a(x - h)^{2} + k $ 的形式为y=−$\frac{1}{4}$(x+2)²+4.

答案： y=−$\frac{1}{4}$(x+2)²+4

3. 二次函数 $ y = \frac{1}{2}x^{2} + 3x + \frac{5}{2} $ 的图象是由函数 $ y = \frac{1}{2}x^{2} $ 的图象先向左(左、右)平移3个单位长度,再向下(上、下)平移2个单位长度得到的.

答案： 左　3　下　2

4. 已知抛物线 $ y = ax^{2} + bx - 3 $ 经过点 $ A(2, - 3) $,$ B(-1, 0) $,则二次函数的解析式为y=x²−2x−3；要使该二次函数的图象与 $ x $ 轴只有一个交点,应把图象沿 $ y $ 轴向上平移4个单位.

答案： y=x²−2x−3　4

5. 已知二次函数 $ y = - \frac{1}{2}x^{2} + 4x - 5 $.
(1) 求该函数图象的顶点坐标和对称轴；
(2) 在平面直角坐标系中画出它的图象.

答案：
解
(1)(方法一)因为−$\frac{b}{2a}$=−$\frac{4}{2×(-\frac{1}{2})}$ = 4，$\frac{4ac−b²}{4a}$=$\frac{4×(-\frac{1}{2})×(-5) - 4²}{4×(-\frac{1}{2})}$ = 3，所以该函数图象的顶点坐标为(4，3)，对称轴为直线x = 4。
(方法二)y = −$\frac{1}{2}$x² + 4x - 5 = −$\frac{1}{2}$(x² - 8x) - 5 = −$\frac{1}{2}$(x - 4)² + 3，所以该函数图象的顶点坐标为(4，3)，对称轴为直线x = 4。
(2)列表如下:
x　　　...　　1　　2　　3　　4　　5　　6　　7　...
y = −$\frac{1}{2}$x² + 4x - 5　...　 - 1.5　1　2.5　3　2.5　1　 - 1.5　...
描点、连线，画出图象如图所示:

1. 二次函数 $ y = ax^{2} + x + 1 $ 的图象必过点(C)
A.$ (0, a) $
B.$ (-1, - a) $
C.$ (-1, a) $
D.$ (0, - a) $

答案： C

2. 已知 $ (-3, y_{1}) $,$ (-2, y_{2}) $,$ (1, y_{3}) $ 是抛物线 $ y = - 3x^{2} - 12x + m $ 上的三点,则(B)
A.$ y_{3} ＜ y_{2} ＜ y_{1} $
B.$ y_{3} ＜ y_{1} ＜ y_{2} $
C.$ y_{2} ＜ y_{3} ＜ y_{1} $
D.$ y_{1} ＜ y_{3} ＜ y_{2} $

答案： B

3. 已知二次函数 $ y = ax^{2} - bx + c(a \neq 0) $ 的图象经过第一象限的点 $ (1, - b) $,则一次函数 $ y = bx - ac $ 的图象不经过(C)
A.第一象限
B.第二象限
C.第三象限
D.第四象限

答案： C

4. 如图,现要在抛物线 $ y = x(4 - x) $ 上找点 $ P(a, b) $,针对 $ b $ 的不同取值,所找点 $ P $ 的个数,三人的说法如下：

甲：若 $ b = 5 $,则点 $ P $ 的个数为 $ 0 $；
乙：若 $ b = 4 $,则点 $ P $ 的个数为 $ 1 $；
丙：若 $ b = 3 $,则点 $ P $ 的个数为 $ 1 $.
下列判断正确的是(C)
A.乙错,丙对
B.甲和乙都错
C.乙对,丙错
D.甲错,丙对

答案： C

5. 某同学利用描点法画二次函数 $ y = ax^{2} + bx + c(a \neq 0) $ 的图象时,列出的部分数据如下表：

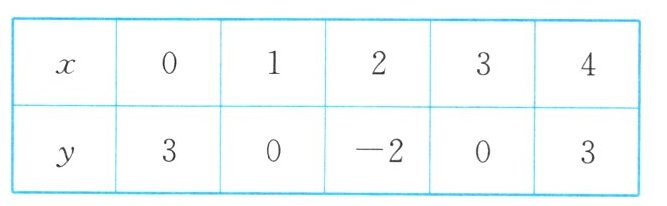
经检查,发现表格中恰好有一组数据计算错误,请你根据上述信息写出该二次函数的解析式：y = x² - 4x + 3.

答案： y = x² - 4x + 3