第86页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的
内接正多边形
,这个圆就是这个正多边形的外接圆
。
答案:
内接正多边形 外接圆
2. 把一个正多边形的外接圆的圆心叫做这个正多边形的
中心
,外接圆的半径叫做正多边形的半径
,正多边形每一边所对的圆心角叫做正多边形的中心角
,中心到正多边形的一边的距离叫做正多边形的边心距
。
答案:
中心 半径 中心角 边心距
3. 若正方形的边长为6,则其半径等于
3$\sqrt{2}$
,边心距等于3
。
答案:
3$\sqrt{2}$ 3
1. 下列说法不正确的是(
A.圆内接正$n边形的中心角为\frac{360^{\circ}}{n}$
B.各边相等,各角也相等的多边形是正多边形
C.各边相等的圆内接多边形是正多边形
D.各角相等的多边形是正多边形
D
)A.圆内接正$n边形的中心角为\frac{360^{\circ}}{n}$
B.各边相等,各角也相等的多边形是正多边形
C.各边相等的圆内接多边形是正多边形
D.各角相等的多边形是正多边形
答案:
D
2. 如图,$A$,$B$,$C$,$D$为一个正多边形的顶点,$O$为正多边形的中心,若$\angle ADB = 18^{\circ}$,则这个正多边形的边数为
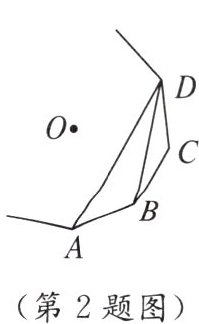
10
。
答案:
10
3. 如图,正十二边形$A_1A_2… A_{12}$,连接$A_3A_7$,$A_7A_{10}$,则$\angle A_3A_7A_{10} = $
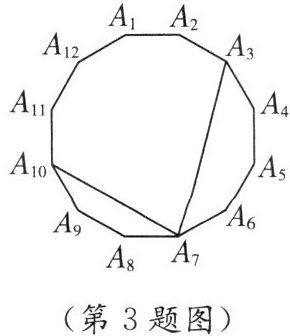
75
$^{\circ}$。
答案:
75
4. 如图,圆内接正八边形$ABCDEFGH$,若$\triangle ADE$的面积为10,则正八边形$ABCDEFGH$的面积为
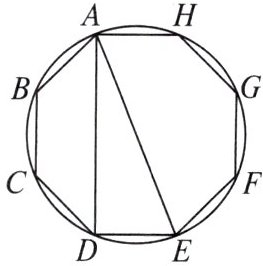
40
。
答案:
40
5. 一个中心角等于$24^{\circ}$的正多边形的边数为
15
;一个外角等于$24^{\circ}$的正多边形的边数为15
。
答案:
15 15
6. 已知正$n边形的边长为a$,边心距为$r$,求正$n边形的半径R$,周长$P和面积S$。
答案:
解:如图,因为OM⊥AB, 所以AM=BM=$\frac{1}{2}$AB=$\frac{1}{2}$a. 在Rt△AOM中,$R=\sqrt{OM^2+AM^2}=\sqrt{r^2+(\frac{1}{2}a)^2}=\sqrt{r^2+\frac{1}{4}a^2}$ 因为正n边形的边长为a, 所以正n边形的周长P=na. 因为$S_{\triangle AOB}=\frac{1}{2}AB\cdot OM=\frac{1}{2}ar$, 所以在正n边形中,这样的三角形共有n个,$S=\frac{1}{2}nar$.
1. 如图,在$\odot O$中,$OA = AB$,$OC\perp AB$,则下列结论错误的是(
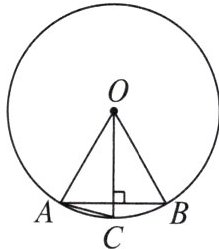
A.弦$AB$的长等于圆内接正六边形的边长
B.弦$AC$的长等于圆内接正十二边形的边长
C.$\overset{\frown}{AC} = \overset{\frown}{BC}$
D.$\angle BAC = 30^{\circ}$
D
)
A.弦$AB$的长等于圆内接正六边形的边长
B.弦$AC$的长等于圆内接正十二边形的边长
C.$\overset{\frown}{AC} = \overset{\frown}{BC}$
D.$\angle BAC = 30^{\circ}$
答案:
D
查看更多完整答案,请扫码查看


