《2025年同步测控优化设计九年级数学上册人教版精编版》

6. 写出一个既有轴对称性质又有中心对称性质的图形名称：圆。

答案： 线段、圆、正方形、矩形、菱形、正2n边形(n为正整数)等(写出其中一个即可)

7. 如图,$ ABCD $ 是一张矩形纸片,点 $ O $ 为矩形对角线的交点,直线 $ MN $ 经过点 $ O $ 交 $ AD $ 于 $ M $,交 $ BC $ 于 $ N $。

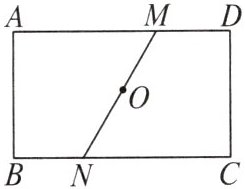
操作：先沿直线 $ MN $ 剪开,并将直角梯形 $ MNCD $ 绕点 $ O $ 旋转 ② 后(填入一个你认为正确答案的序号：① $ 90 ^ { \circ } $；② $ 180 ^ { \circ } $；③ $ 270 ^ { \circ } $；④ $ 360 ^ { \circ } $),恰与直角梯形 $ NMAB $ 完全重合；再将重合后的直角梯形 $ MNCD $ 以直线 $ MN $ 为轴对称翻转 $ 180 ^ { \circ } $ 后所得的图形是下图中的 (4)。(填写正确图形的代号)

答案： ②
(4)

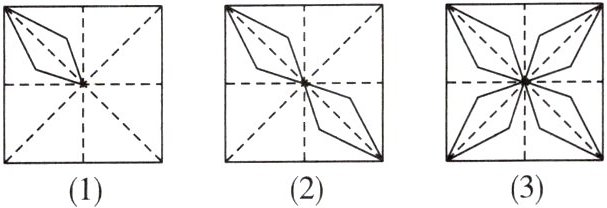
8. 小亮设计地板砖的图案过程如图所示,由图(1)是如何得到图(2)的？由图(2)是如何得到图(3)的？

答案： 解 答案不唯一，如可由图
(1)通过轴对称或中心对称或旋转得到图
(2)，再由图
(2)通过轴对称或旋转得到图
(3).

★9. 如图,方格纸中的每个小方格都是边长为 $ 1 $ 个单位的正方形,$ \mathrm { Rt } \triangle ABC $ 的顶点均在格点上,在建立平面直角坐标系后,点 $ A $ 的坐标为 $ ( - 6,1 ) $,点 $ B $ 的坐标为 $ ( - 3,1 ) $,点 $ C $ 的坐标为 $ ( - 3,3 ) $。

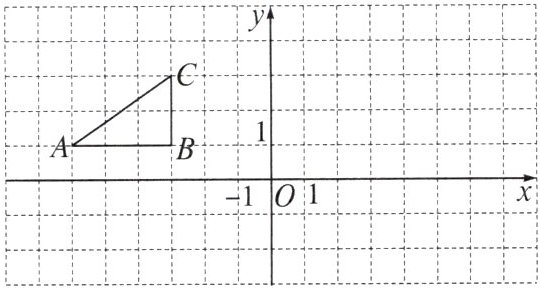
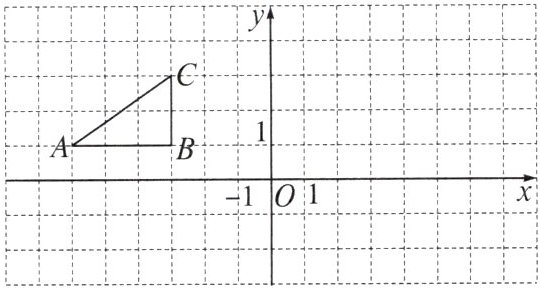
(1)将 $ \mathrm { Rt } \triangle ABC $ 沿 $ x $ 轴正方向平移 $ 5 $ 个单位长度得到 $ \mathrm { Rt } \triangle A _ { 1 } B _ { 1 } C _ { 1 } $,试在图上画出图形 $ \mathrm { Rt } \triangle A _ { 1 } B _ { 1 } C _ { 1 } $,并写出点 $ A _ { 1 } $ 的坐标；
(2)将原来的 $ \mathrm { Rt } \triangle ABC $ 绕点 $ B $ 顺时针旋转 $ 90 ^ { \circ } $ 得到 $ \mathrm { Rt } \triangle A _ { 2 } B _ { 2 } C _ { 2 } $,试在图上画出 $ \mathrm { Rt } \triangle A _ { 2 } B _ { 2 } C _ { 2 } $ 的图形。

答案：
解
(1)A₁(-1,1)，如图；
(2)如图.

10. 如图①,利用左边所给的基本图形可以设计许多富有生活情趣的图案,如图②所示。请你再设计一个图案,并说明它的含义。

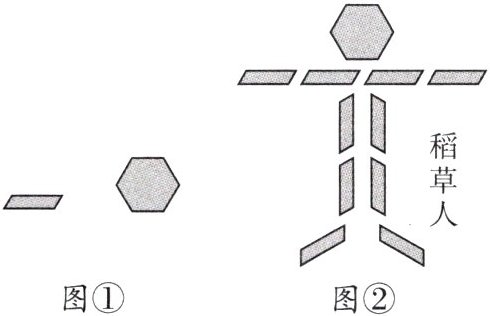
答案：
解 答案不唯一，如下图供参考.