第55页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
2. 如图,$\triangle ABC$ 和 $\triangle AB^{\prime}C^{\prime}$ 成中心对称,点 $A$ 为对称中心,若 $\angle C = 90^{\circ}$,$\angle B = 30^{\circ}$,$AC = 1$,则 $BB^{\prime}$ 的长为(
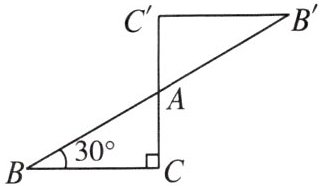
A.4
B.$\frac{\sqrt{3}}{3}$
C.$\frac{2\sqrt{3}}{3}$
D.$\frac{4\sqrt{3}}{3}$
A
)
A.4
B.$\frac{\sqrt{3}}{3}$
C.$\frac{2\sqrt{3}}{3}$
D.$\frac{4\sqrt{3}}{3}$
答案:
A
3. 如图,若甲、乙关于点 $O$ 成中心对称,则乙图中不符合题意的一块是(
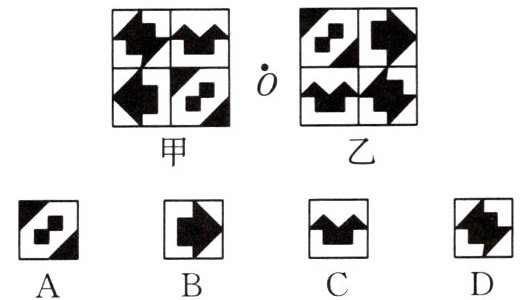
C
)
答案:
C
4. 如图,$\triangle ABC$ 与 $\triangle DEF$ 关于点 $O$ 成中心对称,则图中关于点 $O$ 成中心对称的三角形还有
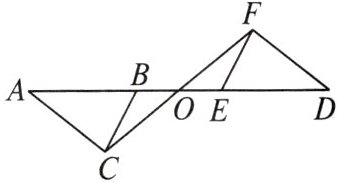
△BOC与△EOF,△AOC与△DOF
。
答案:
△BOC与△EOF,△AOC与△DOF
5. 如图,在等腰三角形 $ABC$ 中,$\angle C = 90^{\circ}$,$BC = 2\ cm$,如果以 $AC$ 的中点 $O$ 为旋转中心,将这个三角形旋转 $180^{\circ}$,点 $B$ 落在点 $B^{\prime}$ 处,那么点 $B^{\prime}$ 与点 $B$ 的距离为
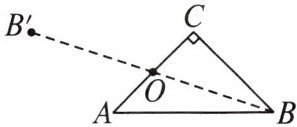
$2\sqrt{5}$
$cm$。
答案:
$2\sqrt{5}$
6. 如图,菱形 $ABCD$ 的对角线的长分别为 2 和 5,$P$ 是对角线 $AC$ 上一点,且 $PE// BC$,交 $AB$ 于点 $E$,$PF// CD$,交 $AD$ 于点 $F$,则阴影部分的面积是______
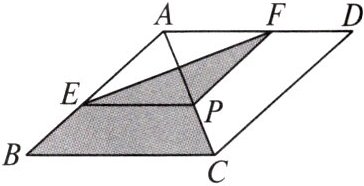
2.5
。
答案:
2.5
7. 如图,已知 $\triangle ABC$ 和点 $P$,求作 $\triangle A^{\prime}B^{\prime}C^{\prime}$,使它关于点 $P$ 与 $\triangle ABC$ 中心对称。
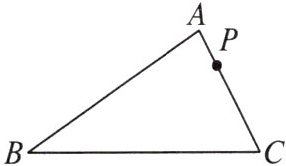

答案:
解 点P在边AC上,只需延长边CA,在直线AC上截取A'P=PA,C'P=PC;连接BP,并延长BP到点B',使B'P= PB;连接A'B',B'C'. 如图,△A'B'C'就是所求作的三角形.
解 点P在边AC上,只需延长边CA,在直线AC上截取A'P=PA,C'P=PC;连接BP,并延长BP到点B',使B'P= PB;连接A'B',B'C'. 如图,△A'B'C'就是所求作的三角形.

8. 下面是小亮同学做的练习。
题目:“如图所示的两个四边形能否关于某一点成中心对称?若能,请你画出其对称中心。”
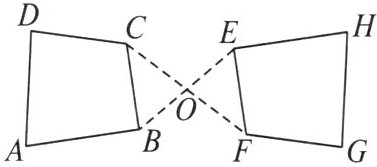
解:如图,连接 $BE$,$CF$ 交于点 $O$,则点 $O$ 就是这两个四边形的对称中心,因此这两个四边形关于点 $O$ 成中心对称。
你认为小亮同学做得是否正确,谈谈你的做法。
题目:“如图所示的两个四边形能否关于某一点成中心对称?若能,请你画出其对称中心。”

解:如图,连接 $BE$,$CF$ 交于点 $O$,则点 $O$ 就是这两个四边形的对称中心,因此这两个四边形关于点 $O$ 成中心对称。
你认为小亮同学做得是否正确,谈谈你的做法。
答案:
解 小亮的做法不正确.正确做法应为:如图,连接AH,DG,BE,CF,交于一点O,经测量CO=FO,BO=EO,AO=HO,DO=GO,所以四边形ABCD与四边形HEFG关于点O成中心对称.
解 小亮的做法不正确.正确做法应为:如图,连接AH,DG,BE,CF,交于一点O,经测量CO=FO,BO=EO,AO=HO,DO=GO,所以四边形ABCD与四边形HEFG关于点O成中心对称.

9. 如图,跷跷板的支柱 $OC$ 与地面垂直,点 $O$ 是 $AB$ 的中点,$AB$ 可以绕着点 $O$ 上下转动。如果 $\angle OCA = 90^{\circ}$,当 $A$ 端落地时,$\angle OAC = 25^{\circ}$,问小孩玩跷跷板时:
(1)在空中划过怎样的线?
(2)横板上下可转动的最大角度(即 $\angle A^{\prime}OA$)是多少?
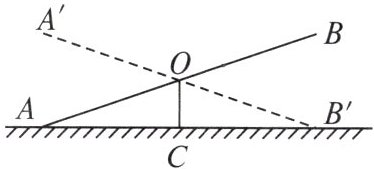
(1)在空中划过怎样的线?
(2)横板上下可转动的最大角度(即 $\angle A^{\prime}OA$)是多少?

答案:
解
(1)如图,在空中划过一段以O为圆心,以OA为半径的弧线.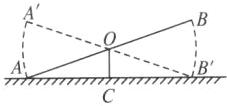
(2)$\angle AOA'=\angle BOB'=\angle BAC+\angle A'B'C=25°+25°=50°$.
解
(1)如图,在空中划过一段以O为圆心,以OA为半径的弧线.

(2)$\angle AOA'=\angle BOB'=\angle BAC+\angle A'B'C=25°+25°=50°$.
查看更多完整答案,请扫码查看


